В предыдущих параграфах мы выяснили, что работа любой системы массового обслуживания (СМО) состоит в выполнении поступающего в нее потока заявок. Заявки поступают одна за другой в некоторые, вообще говоря, случайные моменты времени. Обслуживание поступившей заявки продолжается некоторое время, после чего канал (обслуживающая единица СМО) и снова готов для приема следующей заявки. На практике обычно случайны не только моменты поступления заявок, но и по большей степени длительность обслуживания заявки. В связи с этим процесс работы системы протекает нерегулярно: в потоке заявок образуются местные сгущения и разрежения. Сгущения могут привести либо к отказам в обслуживании, либо к образованию очередей. Разрежения могут привести к непроизводительным простоям отдельных каналов или системы в целом. На эти случайности, связанные с неоднородностью потока заявок, накладываются еще случайности, связанные с задержками обслуживания. Таким образом, процесс функционирования СМО представляет собой случайный процесс. Чтобы дать рекомендации по рациональной организации системы, выяснить ее пропускную способность, т.е. степень приспособленности системы к выполнению потока заявок, и предъявить к ней требования, необходимо изучить случайный процесс, протекающий в системе и описать его математически.
Случайный процесс, протекающий в СМО, состоит в том, что система в случайные моменты времени переходит из одного состояния в другое: меняется число занятых каналов, число заявок, стоящих в очереди и т.д. Такой процесс существенно отличается от случайных процессов, которые мы рассматривали в главах I-II, т.к. СМО представляет собой физическую систему дискретного типа с конечным (или счетным) числом состояний, а переход системы из одного состояния в другое происходит скачком, в момент, когда осуществляется какое-либо событие (приход новой заявки, освобождение канала, уход заявки из очереди и т.п.).
Рассмотрим физическую систему Х со счетным множеством состояний
х 1, х 2, …, х n, …
В любой момент времени t система может находиться в одном из этих состояний. Обозначим pk (t) (k = 1, 2, …, n, …) вероятность того, что в момент времени t система будет находиться в состоянии хk. Очевидно, что для любого t
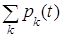 = 1.
= 1.
Совокупность вероятностей pk (t) для каждого момента времени t характеризует данное сечение случайного процесса, проходящего в системе.
Случайные процессы со счетным множеством состояний бывают двух типов: с дискретным и непрерывным временем. Первые отличаются тем, что переходя из состояния в состояние могут происходить только в строго определенные, разделенные конечными интервалами моменты времени t 1, t 1, … Случайные процессы с непрерывным временем отличаются тем, что переход системы из состояния в состояние возможен в любой момент времени t.
Случайные процессы, протекающие в СМО, как правило, представляют собой процессы с непрерывным временем, что связано со случайностью потока заявок. Также отметим, что для СМО характерны обратимые переходы: занятый канал может освободиться, очередь может «рассосаться» и т.п. (в отличие от необратимых переходов, как например, сбитый во время воздушного боя самолет в бой уже не возвращается).
В качестве примера рассмотрим следующую дискретную систему с непрерывным временем: одноканальную систему обслуживания, которая может находиться в четырех состояниях
х 0 – канал исправен и свободен,
х 1 – канал исправен и занят,
х 2 – канал неисправен и ждет ремонта,
х 3 – канал неисправен и ремонтируется.
Составим для этого случая схему переходов
 |
Заметим, что во-первых, предполагается, что неработающий канал выйти из строя не может, во-вторых, что переход системы из х 3 непосредственно в х 1, минуя х 0, можно считать практически невозможным, так как для этого нужно, чтобы окончание ремонта и приход очередной заявки произошли строго в один момент времени.
Для того, чтобы описать случайный процесс, протекающий в СМО с непрерывным временем, прежде всего нужно проанализировать причины, вызывающие переход системы из состояния в состояние. Для СМО основным фактором, обуславливающим протекающие в ней процессы, является поток заявок.






