1. Вероятности перехода в простой однородной цепи Маркова задаются матрицей
Р 1 = 
.
Чему равно количество состояний для этой цепи? Найти матрицу перехода из состояния в состояние за три шага.
2. Состояния банка s 1, s 2, s 3, s 4 характеризуются процентными ставками 2%, 3%, 5% и 8% соответственно, которые устанавливаются в начале каждого месяца и фиксированы на всем его протяжении. Наблюдение за работой банка в предшествующий период показало, что переходные вероятности состояний в течение квартала изменяются пренебрежимо мало. Следовательно, их можно считать постоянными.
Определить вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 5%, а размеченный граф состояний банка имеет вид
 |
Ответ. В последнем месяце рассматриваемого квартала процентные ставки 2%, 3%, 5%, 8% будут соответственно с вероятностями 0,170; 0,456; 0,245; 0,129. Таким образом, в последнем месяце квартала вероятнее всего процентная ставка будет 3%.►
3. Состояния банка s 1, s 2, s 3, s 4 характеризуются процентными ставками 3%, 4%, 5% и 6% соответственно, которые устанавливаются в конце каждого месяца. Переходные вероятности зависят от моментов установления процентных ставок, причем матрицы переходных вероятностей задаются следующим образом:
Р(1)= 
,Р(2)= 
, Р(3)= 
.
Построить размеченные графы состояний, соответствующие началам каждого месяца в квартале, и найти вероятности состояний банка в конце квартала, если в конце предшествующего квартала процентная ставка составляла 3%.
Ответ. В конце квартала процентные ставки составят 3%, 4%, 5%, 6% соответственно с вероятностями 0.16; 0,14; 0,47; 0,23, т.е. наиболее вероятна ставка 5%.
4. Задан следующий размеченный граф состояний
 |
|
|
|
|
|
|
|
 | |||
| |||
Составить уравнения и найти предельные вероятности состояний.
5. Каждый из двух банков А и В может пребывать в одном из двух состояний, характеризующихся процентными ставками по вкладам, которые устанавливаются в начале квартала и сохраняются неизменными на всем его протяжении: состояние s 1 – процентная ставка 5%, состояние s 2 – процентная ставка 6%. Вероятности переходов банков А и В из состояния в состояние не зависят от времени и задаются соответственно матрицами
РА = 
и РВ = 
.
Построить размеченные графы состояний банков. Найти финальные вероятности состояний для каждого банка и дать рекомендации вкладчикам по выгодности вкладов по банкам.
Ответ. Финальные вероятности банка А: р 1 = 
, р 2 = 
;
Финальные вероятности банка В: р 1 =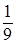 
, р 2 = 
.
Глава вторая
Основы теории массового обслуживания.
Введение.
Ожидание того или иного вида обслуживания является частью нашей повседневной жизни. Мы ожидаем, чтобы пообедать в ресторане, стоим в очереди в кассах супермаркетов, ожидаем приема в поликлинике и т.д. Однако феномен ожидания характерен не только для людей, например, работы, поставленные в очередь для выполнения на станке, группа пассажирских самолетов, поставленная в очередь на ожидание взлета, автомобили, движение которых приостановлено сигналом светофора и т.п. К сожалению феномен ожидания нельзя исключить без чрезмерных расходов. И только на одно мы можем надеяться - на возможность сокращения времени ожидания в очереди до некоторых терпимых пределов.
Изучение очередей в системах массового обслуживания позволяет определить критерии функционирования обслуживающей системы, среди которых наиболее значимыми являются среднее время ожидания в очереди и средняя длина очереди. Эта информация используется затем для выбора надлежащего уровня обслуживания.
Пример. Посетители ресторана быстрого питания жалуются на медленное обслуживание. В настоящее время в ресторане работают три кассира. Управляющий поручил консалтинговой фирме провести расследование жалобы. В результате была обнаружена следующая зависимость между числом кассиров и временем ожидания обслуживания.
| Число кассиров | |||||||
| Среднее время ожидания (минуты) | 16,2 | 10,3 | 6,9 | 4,8 | 2,9 | 1,9 | 1,3 |
Приведенные данные свидетельствуют о том, что при работающих в настоящее время трех кассирах среднее время ожидания равно примерно 7 минут. Управляющий хочет уменьшить время ожидания до трех минут. Как следует из этих же данных, время ожидания становится менее трех минут, если число кассиров больше или равно пяти.
Результаты исследования системы обслуживания также можно использовать для оптимизации модели со стоимостными характеристиками, в которых минимизируется сумма затрат, связанных с предоставлением услуг, и потерь, обусловленных задержками в их предоставлении.
На данном рисунке изображена типичная стоимостная модель системы обслуживания (в долларах на единицу времени), где затраты на обслуживание возрастают с ростом его уровня. В то же время потери, обусловленные задержками в предоставлении услуг, уменьшаются с возрастанием уровня обслуживания. Главной проблемой, связанной с применением стоимостных моделей, является трудность оценки потерь в единицу времени, обусловленных задержками в предоставлении услуг.
