Все процессы, протекающие в цепях синусоидального тока, значительно сложнее тех, которые наблюдаются в цепях постоянного тока. Во-первых, в таких цепях различают уже не один, а три основных элемента: активные сопротивления R, индуктивность L и емкость С; во-вторых, переменные синусоидальные токи и напряжения вызывают периодические изменения энергий, которые запасаются в электрическом поле емкостных элементов (конденсаторах) WЭ =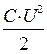 
и в магнитном поле индуктивных элементов (катушек) WМ = 
.
При этом емкостные (С) и индуктивные (L) элементы обмениваются энергиями друг с другом и с источником, а на активных сопротивлениях электрическая энергия преобразуется в другие виды энергии. Именно перераспределением энергии и определяются соотношения между током и напряжением на отдельных элементах:
на активном R: UR = i·R; (6.1)
на индуктивном L: UL =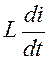 
; (6.2)
на емкостном С: UC = 
. (6.3)
Из этих соотношений вытекает, что только на активном сопротивлении синусоиды тока и напряжения совпадают по фазе, на индуктивном – синусоида напряжения опережает синусоиду тока на 900; на емкости, наоборот, синусоида напряжения отстает от синусоиды тока на 900. В таблице 13 приведены основные характеристики элементов цепей синусоидального тока.
Таблица 13 – Характеристики основных элементов цепей
синусоидального тока
| Характеристики | R | L | С |
| 1. Напряжение на зажимах при синусоидальном токе i = Im·sinω·t | U = Umsinω·t | U=Umsin(ωt +  )
| U= Umsin(ωt - )
|
| 2. Закон Ома для участка цепи для действующих значений тока и напряжения | I = 
| I =  ;
ХL= ω·L
| I =  ;
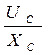ХC = 
|
| 3. Угол сдвига фаз между синусоидами напряжения и тока φ = φu – φi | φ = 0 | φ = 
| φ =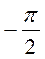 
|
| 4. Активная мощность, выделяемая в элементе Р = U· I cos φ | P = I2·R= U·I = = 
|
Продолжение таблицы 13
| Характеристики | R | L | С |
| 5. Реактивная мощность элемента Q = U· I sin φ |  0
| QL= I2·XL=
= UL·I= 
| QC= -I2·XC =
=-UC·I = 
|
| 6. Векторная диаграмма напряжения и тока | 
| 
| |
| 7.Сопротивления в символической форме | R | XL= jωL | XC =
= - j 
|
При последовательном соединении трех названных идеальных элементов (рис.24) уравнение для мгновенных значений напряжений в соответствии со 2-м законом Кирхгофа U = UR+UС+UL.
В комплексной форме для действующих значений
Ú = ÚR + ÚL + ÚC = IR + I j ωL + I(– j 
) = I Z, (6.4)
где Z – комплекс полного сопротивления цепи (Ом):
Z = Zejφ, (6.5)
где Z = 
– модуль полного сопротивления,
φ – угол сдвига фаз между синусоидами тока и напряжения (аргумент комплексного сопротивления):
. (6.6)
 |
Рисунок 24 – Схема электрической цепи с последовательным включением R, L, C элементов
В приведенных соотношениях XL-XС – результирующее реактивное сопротивление цепи, обозначающее характер нагрузки цепи: если XL > ХС, нагрузка имеет индуктивный характер, при этом угол сдвига фаз φ считают условно положительным (φ>0); если XL<ХСφ<0, нагрузка носит емкостной характер, и угол φ считают условно отрицательным (φ < 0).
На рис. 25, а, б приведены векторные диаграммы напряжений и тока для, соответственно, индуктивного и емкостного характера нагрузки.
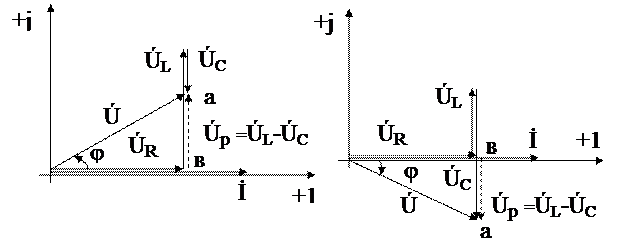
φ > 0
а б
а – при индуктивном характере нагрузки;
б – при емкостном характере нагрузки.
Рисунок 25 – Векторные диаграммы напряжений и тока для последовательной цепи с R,L,C – элементами.
Векторные прямоугольные треугольники оав называют треугольниками напряжений, в этих треугольниках активные составляющие полного напряжения Vа совпадают по направлению с вектором тока, реактивные – в зависимости от характера нагрузки, при индуктивном характере – опережают, при емкостном – отстают.
На рис. 26 показан треугольник напряжений при индуктивном характере нагрузки.
Разделив каждую сторону векторного треугольника напряжений на вектор тока, получим скалярный прямоугольный треугольник сопротивлений 0' а' в', гипотенуза представляет полное сопротивление цепи z, а два катета – активное R и реактивное X сопротивления цепи.
 | |||
 | |||
а б в
Рисунок 26 – Треугольники напряжений, сопротивлений, мощностей
Из треугольника напряжений (рис. 26а) активная и реактивная составляющие напряжений определяются по следующим формулам:
Up = UL – UC; Up = U·sinφ. (6.7)
Ua = U·cosφ (6.8)
Из треугольника сопротивлений (рис. 26б) активная и реактивная составляющие сопротивлений определяются по следующим формулам:
X= XL – XC; X = z·sinφ. (6.9)
R = z·cosφ (6.10)
Из треугольника мощностей (рис. 26в) активная, реактивная и полная мощность определяются по следующим формулам:
P = U·I·cosφ = I2 ·R = Ua ·I (6.11)
Q = QL – QC; Q = I2 ·X = U·I·sinφ = Up·I (6.12)
S = U·I = I2 ·z = 
(6.13)
Если каждую сторону векторного треугольника напряжений 0''а''в'' умножить на вектор тока, получим прямоугольный скалярный треугольник мощностей, где в масштабе мощностей гипотенуза представляет полную мощность цепи S, а два катета – активную Р и реактивную Q мощности цепи.
Анализ электрических цепей синусоидального тока, как правило, сопровождается построением векторных диаграмм с активными и реактивными составляющими напряжения, что повышает наглядность результата расчета. Для расчета цепей и построения векторных диаграмм необходимо уметь определить параметры приемников.
