Проведение эксперимента и обработка данных

 

1 Исследовать последовательное включение катушки и резистора, для чего включить ту же катушку последовательно с резистором в соответствии со схемой (рис. 27).

 

Рисунок 27 – Цепь с последовательным включением резистора и катушк и

 

Измерить ток, напряжение цепи, напряжение на резисторе и катушке, данные занести в таблицу 15. Рассчитать параметры катушки, а также все другие величины, приведенные в таблице 15

Таблица 15 – Результаты измерений

№	Измерено	Вычислено
I	U	UR	UK	Для катушки
ZK	RK	XK	LK	φ	Uak	Uрк
	А	В	В	В	Ом	Ом	Ом	Гн	гр	В	В

Продолжение таблицы 15

 

Вычислено
Для всей цепи
Z	RΣ	φ	Ua	Up	PR	PK	P	Q	S
Ом	Ом	гр	В	В	Вт	Вт	Вт	ВАр	ВА

2 Для определения параметров катушки необходимо построить векторную диаграмму, используя напряжения U, U_R, U_k (рис. 28).

Из векторной диаграммы следует:

 

 

U² = (U_R + U_ak)² + U²_pk = U²_R + 2U_R·U_ak + U²_ak + U²_pk. (6.14)

 

ввиду того, что U²_ak + U²_pk = U²_k, получим:

 

U² = U²_R + 2U_R·U_ak + U²_{k .}(6.15)

 

 

 

 

 

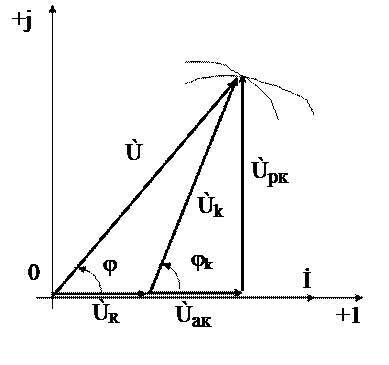Рисунок 28 – Векторная диаграмма для определения параметров катушки

 

Отсюда активная и реактивная составляющие напряжения катушки:

 

U_ak = 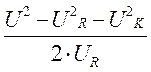; U_pk = 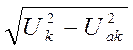(6.16)

 

Другие величины могут быть вычислены используя следующие формулы:

 

Z_k = ; (6.17)

 

R_R= ; (6.18)

 

R=R_R+R_K; (6.19)

 

X_К = Z_K·sinφ_K = ; (6.20)

 

L_K = ; (6.21)

 

U_a = U·cosφ; (6.22)

 

U_ak = R_K· I; (6.23)

 

U_p = U·sinφ; (6.24)

 

φ = arctg ; (6.25)

 

φ_k = arctg 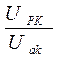; (6.26)

 

P_R = U_R·I = I²·R; (6.27)

 

P = U·Icosφ = I²·R; (6.28)

 

P = P_R+P_K; (6.29)

 

Q = U·Isinφ = I²· X_К; (6.30)

 

S = U·I = 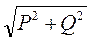; (6.31)

 

U_Lk = U_p. (6.32)

 

Z = (6.33)

 

3 Исследовать цепь с последовательным соединением резистора и конденсатора. Собрать цепь (рис. 29), произвести измерение тока и напряжения при двух значениях напряжения. Данные эксперимента занести в таблицу 16. Вычислить параметры цепи, активные и реактивные составляющие напряжения, мощности и угла сдвига фаз. Построить векторную диаграмму напряжения, вид которой представлен на рисунке 30.

 

 

 

 

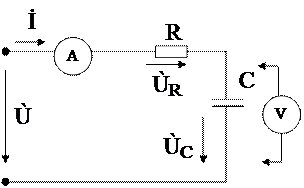
Рисунок 29 – Последовательное соединение резистора и конденсатора

 

 

 

Рисунок 30 – Векторная диаграмма напряжений

 

Таблица 16 – Результаты измерений и анализа

 

№

Измерено

Вычислено

U, B

I, A

UR, B

UC, B

Р, Вт

Z Ом

R, Ом

ХС, Ом

С, Ф

φ, град

Р, Вт

Q, BAp

S, BA

 

4 Исследовать последовательное соединение резистора, катушки индуктивности и конденсатора. Собрать цепь (рис. 31), используя элементы, параметры которых были определены ранее. Рекомендуется проводить опыт в следующей последовательности. Изменяя значение емкости, найти режим с наибольшим значением тока (режим резонанса, когда X_L = X_C). Затем, увеличивая емкость, получить режим работы цепи с индуктивным характером нагрузки (X_L > X_C). Вернуться к режиму резонанса напряжения и, уменьшая значение емкости, получить режим работы цепи с емкостным характером нагрузки (X_L < X_C). И в том и в другом случае измерить ток и напряжение, данные занести в таблицу 17.

 

Рисунок 31 – Последовательное соединение резистора, катушки индуктивности и конденсатора

Таблица 17 – Результаты измерений и анализа

 

№	Измерено	Вычислено
U, В	I, А	UR, В	UК, В	UС, В	Р, Вт	Z, Ом	R, Ом	Х, Ом

Продолжение табл. 17

Uрк, В Uaк, В Ua, В ±Uр, В φ, град Р, Вт Q, ВАр S, ВА

 

Рассчитать величины, обозначенные в таблице, построить векторные диаграммы напряжений для режимов X_L > X_C и X_L < X_C так, как показано на рисунке 32. Построить треугольники сопротивлений и мощностей.

 

 

 

а

 

б

а – для индуктивного характера нагрузки;

б – для емкостного характера нагрузки

Рисунок 32 – Векторные диаграммы для цепи, изображенной на рис.31

 

Контрольные вопросы

1 Какие процессы происходят на активном, индуктивном и емкостном элементах в цепи синусоидального тока?

2 Как определить индуктивное и емкостное сопротивление по заданным значениям L, C и частоты f?

3 Как определить параметры цепи синусоидального тока при наличии амперметра, вольтметра и ваттметра?

4 Как определить параметры цепи синусоидального тока при наличии только амперметра и вольтметра?

5 Каким соотношением определяется полное сопротивление цепи при наличии R, L, C элементов?

6 Как определить активные и реактивные составляющие напряжений, сопротивлений, мощностей, если известные полные значения указанных величин и углы сдвига фаз между синусоидами тока и напряжения?

7 Как сдвинуты относительно друг друга синусоиды (векторы) тока и напряжения на R, L, C элементах в цепи синусоидального тока?

8 Можно ли представить цепь, изображенную на рис.24, эквивалентной схемой замещения, состоящей только из двух элементов – активного и реактивного? Как определить параметры такой схемы замещения, используя векторную диаграмму, построенную для исходной цепи?

Литература

 

1 Рибалко, М. П. Теоретичні основи електротехніки. Лінійні електричні кола: підручник / М. П. Рыбалко, В. О. Єсауленко, В. І. Костенко. – Донецьк: Новий світ, 2003. – C.86-89.

2 Бессонов, Л. А. Теоретические основы электротехники. Электрические цепи: учебник / Л. А. Бессонов. – 10-е изд. – М.: Гардарики, 2002. – С.97-100. – ISBN 5 – 8297 – 0026 – 3.

Лабораторная работа 6