Краткие теоретические сведения. Элементы, сопротивления которых зависят от величины тока или напряжения на его зажимах, называются нелинейными (Н.Э.)

Элементы, сопротивления которых зависят от величины тока или напряжения на его зажимах, называются нелинейными (Н.Э.). Вольтамперные характеристики (В.А.X.) таких элементов являются нелинейными. Если в электрической цепи содержится хотя бы один нелинейный элемент, вся цепь считается нелинейной. Из-за нелинейности В.А.Х. нелинейные цепи аналитическим путем рассчитываются только в случаях, когда их В.А.Х. с требуемой степенью точности можно аппроксимировать аналитическими функциями, или связь между напряжением и током имеет аналитическую зависимость. Чаще всего расчет нелинейных цепей осуществляют графически. Для этого экспериментально снимают В.А.Х. нелинейных элементов, со­держащихся в цепи, и путем их графического сложения получают результи­рующую В.А.Х. цепи в целом. Получение результирующей В.А.X. является решением задачи по расчету нелинейной цепи, так как используя эту В.А.Х., для заданного напряжения цепи можно определить все неизвестные токи и напряжения на отдельных ее участках.

На рисунке 20 показано построение результирующих В.А.Х. при раз­личных способах соединения нелинейных элементов.

 

 

а

 

`

 

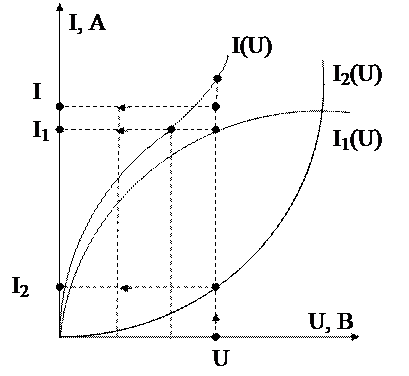б

 

 

 

в

Рисунок 20 – Построение результирующих ВАХ

при различных способах соединения нелинейных элементов:

а – при последовательном; б – при параллельном; в – при смешанном соединении нелинейных элементов

 

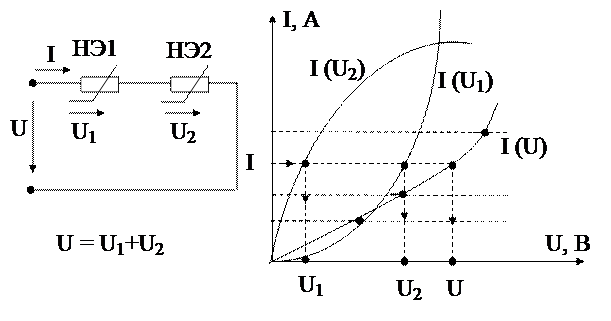
При последовательном соединении (рис. 20, а) на основании вто­рого закона Кирхгофа U = U₁+U₂.

Для получения результирующей В.А.Х. I(U) задаются несколькими произвольными значениями тока и суммируют абсциссы заданных кривых I(U₁) I(U₂).

При параллельном соединении Н.Э. (рис. 20, б) в соответствии с первым законом Кирхгофа I= I₁ + I₂.

Результирующую В.А.Х. I(U) цепи получают сложением ординат зави­симостей I₁(U)n I₂(U) для произвольно взятых значений напряжения U.

При смешанном соединении Н.Э. (рис. 20 в) вначале получают В.А.Х. параллельного участка I₁(U₂₃), а затем, используя зависимости I₁(U₁₂) и I₁(U₂₃), получают результирующую В.А.Х. всей цепи, как двух Н.Э., соединенных последовательно.

Графический расчет нелинейной цепи методом двух узлов показан на рис. 20, а, б. При известных зависимостях I₁(U₁), I₂(U₂), I₃(U₃) на первом этапе выполняют построение зависимостей I₁(U_ав), I₂(U_ав), I₃(U_ав), используя выражения для каждой параллельной вет­ви, составленные с помощью второго закона Кирхгофа:

 

U_ав = Е₁- U_1, (5.1)

 

U_ав = U_2, (5.2)

 

U_ав = Е₃ – U_3. (5.3)

 

На втором этапе необходимо определить такое значение U_ав, при котором выполняется первый закон Кирхгофа для данной расчетной цепи:

 

I₁+I₃= I₂. (5.4)

 

Можно определить это напряжение методом подбора, лучше – вначале по­строить зависимость (I₁ + I₃)=f(U_ав). Точка пересечения кривых I₂(U_ав) и (I₁+I₃) = f(U_ав) и будет являться решением задачи (m.А).