Цель работы: исследовать явления, имеющие место в цепи переменного тока при параллельном включении приемников, научиться определять активные и реактивные составляющие токов в ветвях и всей цепи, строить векторные диаграммы токов для параллельного соединения.
Краткие теоретические сведения
При параллельном соединении приемников, как и в цепи постоянного тока, удобнее пользоваться величинами проводимостей, а также активными Iа и реактивными Iр составляющими тока. На рис. 33, а, б представлена схема электрической цепи с двумя параллельными ветвями, в каждой из которых имеются активные и реактивные элементы, а также векторная диаграмма токов и напряжения для этой цепи.
На приведенной векторной диаграмме изображены треугольники токов:
Δ оес – для первой параллельной ветви с элементами R1, L;
Δ сda – для второй параллельной ветви с элементами R2, С;
Δ ова – для всей ветви с двумя параллельными ветвями.
Если каждую сторону векторного треугольника токов (рис. 34) разделить на вектор напряжения, получим прямоугольный скалярный треугольник проводимостей, гипотенузой которого в масштабе проводимостей является полная проводимость цепи у, катетами – активная g и реактивная в проводимости.
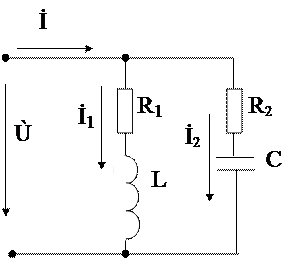
а
а
б
а – схема электрической цепи с параллельными ветвями;
б – векторная диаграмма для приведенной цепи
Рисунок 33 – Схема электрической цепи с параллельными ветвями
и векторная диаграмма токов для этой цепи
 | |||
 | |||
Рисунок 34 – Треугольники токов и проводимостей
Активная и реактивная составляющие тока первой ветви:
Ia1 = I1·cosφ1 = 
; (7.1)
Ip1(L) = I1·sinφ1 = 
; (7.2)
где 
; 
– следует из треугольника сопротивлений, построенного для первой ветви;
g1 = 
– активная проводимость первой ветви (
);
b1(L) = 
– реактивная проводимость первой ветви (индуктивного характера) ().
Аналогично для второй ветви:
İа2 = İ2·cosφ2 = 
; (7.3)
Ip2(C) = I2·sinφ2 = 
; (7.4)
где g2 = 
– активная проводимость второй ветви;
b2(C) = 
– реактивная проводимость второй ветви (емкостного характера).
Из Δ ова полный ток можно представить:
İ = 
=
= 
= U·y12 (7.5)
где y12 – полная проводимость всей цепи ().
Полное сопротивление цепи (рис. 33) определяется как обратная величина полной проводимости y12:
Z12 = 
(7.6)
Углы сдвига фаз можно определить:
– между напряжением и током первой ветви как:
φ1 = arctg 
= arctg 
= arcos 
= arcos 
=arcsin 
=
= arcsin 
; (7.7)
–
между напряжением и током второй ветви как:
φ2 = arctg 
= arctg 
= arcos 
= arcos 
=arcsin 
=
= arcsin 
(7.8)
где у1 = 
, (7.9)
у2 = 
; (7.10)
– между напряжением и полным током цепи как:
φ = arctg 
= arctg 
= arcos 
= arcos 
=arcsin 
=
= arcsin 
(7.11)
где Ip = Ip1 (L) - Ip2 (C) (7.12)
Ia= Ia1 + Ia2 (7.13)
