Резонансом напряжения называют такой режим работы цепи с последовательно соединенными элементами L, R, С, когда угол сдвига фаз между током и напряжением, приложенным к цепи, равен нулю. Условие резонанса напряжения: XL = XC или ω·L = 
. Сопротивление цепи при резонансе: Zрез = 
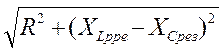= R, т.е. принимает минимальное значение. Ток при резонансе достигает максимального значения: I = 
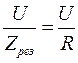. Из условия резонанса вытекает, что резонанс напряжения можно получить, изменяя либо индуктивность L, либо емкость С, либо частоту ω. Собственная частота цепи обозначается ω0 и определяется из выражения
ω0 = 
(8.1)
Различают три признака резонанса: экстремальный, когда ток в цепи равен максимальному (Iрез = Imax); частотный, когда частота, при которой наступает резонанс, равна собственной частоте цепи (ωрез = ω0); фазовый, когда угол сдвига фаз между током и полным напряжением равен нулю (φ =0). Все три признака совпадают только в простейшей цепи – с последовательным соединением трех элементов: L, R, С, в большинстве сложных цепей в обязательном случае может проявиться только один – фазовый, его называют главным признаком резонанса.
Сопротивление реактивных элементов при резонансе называют волновым или характеристическим сопротивлением резонансного контура (цепи):
ρ = ω0·L = 
. (8.2)
Отношение характеристического сопротивления к активному сопротивлению называют добротностью контура или коэффициентом резонанса:
Q = 
. (8.3)
В случае, когда ρ > R, напряжение на индуктивности и емкости в момент резонанса может в несколько раз превышать напряжение, приложенное к цепи. Зависимость сопротивления цепи от частоты называют частотными характеристиками, а действующие значения тока и напряжения от частоты ω – резонансными кривыми (соответственно, рис. 38, 39).
 |
Рисунок 38 – Частотные характеристики резонансного контура
На рисунке 38 представлен ряд резонансных кривых токов контуров с разной добротностью. Чем больше добротность Q, тем острее резонансная кривая тока, тем лучше избирательные свойства цепи.
 |
Рисунок 39 – Резонансные кривые резонансного контура
(зависимость от частоты)
Для оценки избирательных свойств цепи вводят условное понятие ширины резонансной кривой, или полосы пропускания контура, которую определяют как разницу частот, амплитудного и действующего значения тока, отношение 
превышает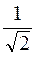 
.
Избирательные свойства резонансных контуров широко используются в электросвязи и радиотехнике, где режим резонанса есть полезным режимом работы. В устройствах, где резонансный режим не предусмотрен, появление резонанса нежелательно, потому что возникают значительные напряжения на катушке и конденсаторе и могут быть нежелательными для изоляции. На рисунке 40 предоставлены резонансные кривые тока контуров разной добротности.
 |
Рисунок 40 – Резонансные кривые тока для контуров разной добротности
В лабораторных условиях режима резонанса чаще всего достигают при помощи конденсатора переменной емкости. В этом случае графики изменения напряжения и тока строятся в зависимости от емкости, а не от частоты. Такие зависимости, представленные на рисунке 41, называются резонансными кривыми.
Основное отличие этих кривых от тех, которые построены в зависимости от частоты, то, что при увеличении емкости С емкостное сопротивление уменьшается и, достигая малых значений, практически не влияет на величину тока, а также на величину индуктивности UL и активного напряжения Ua.
 |
Рисунок 41 – Резонансные кривые (зависимость от емкости)
