ПЗ №1. Линейная алгебра с элементами аналитической геометрии.
1Разбор домашнего задания №1.
2) Найти произведение двух квадратных матриц одного порядка: С=АВ, где 
2) Умножить матрицу А на В: С=АВ: 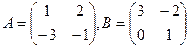
3) Привести матрицу А к ступенчатому виду и определить ее ранг: 
ПЗ№2. Методом Гаусса найти матрицу, обратную матрице 
5) Вычислить матрицу А-1, обратную матрице 
6) Найти общее или единственное решение однородых систем: 

7) Вычислить определители заданных матриц:

ПЗ №3. Элементы векторной алгебры и матричного анализа. Элементы аналитической геометрии.
3. Разбор домашнего задания №2
4. 1) Даны векторы 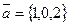 и
и 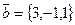 . Найти косинус угла между векторами
. Найти косинус угла между векторами 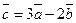 и
и  .
.
2) При каком значении 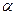 векторы
векторы 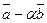 и
и  ортогональны (угол между ними равен
ортогональны (угол между ними равен 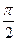 )? Векторы
)? Векторы 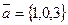 и
и 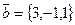 .
.
3) Вычислить угол между векторами  и
и 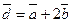 , если
, если 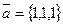 ,
, 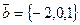 .
.
ПЗ№4. Составить уравнения всех сторон треугольника АВС, где А(3,2), В(5,-2) и С(5,2). Найти их длины.
5) Через точки А(1,-2) и В(5,4) проведена прямая. Составить уравнения прямых, проходящих через точку С(-2,0) перпендикулярно и параллельно прямой АВ. Вычислить растояние от точки С до прямой АВ.
6) Привести к каноническому виду уравнение кривой 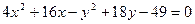 . Определить ее тип, вычислить основные параметры.
. Определить ее тип, вычислить основные параметры.
7) Написать уравнение прямой, проходящей через точку М0(-1,2,1) и
а) имеющий направляющий вектор  ;
;
b) перпендикулярной плоскости 3x-y-2z+1=0;
с) проходящей через точку М0 и М1(3,2,4).
ПЗ № 5. Введение в анализ. Пределы и непрерывность.
3. Разбор домашнего задания №3
4. Найти пределы: 1)  ; 2)
; 2) 
3)  ; 4)
; 4)  ; 5)
; 5) 
6)  ; 7)
; 7) 
ПЗ №6. Дифференциальное исчисление функции одной переменной.
Производная. Дифференциал функции.
3. Разбор домашнего задания №4
4. Пользуясь определением производной, найти производный функций: 1) y=C, где C=const; 2) 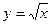 ; 3) y=sinx
; 3) y=sinx
Найти производные функций и вычислить их значения при x=2 и x=0:
1)  ; 2)
; 2)  ; 3)
; 3) 
Найти производные следующих функций: 1) y=sin5x; 2) y=cos5x; 3) y=ln(x2+1); 4) y=78x-3; 5) y=(1-2x)50
ПЗ 7-8. Приложение производной. Функции нескольких переменных.
3. Разбор домашнего задания №5
4. 1) Найти интервалы монотонности и точки эксремума функции  . Вычислить наибольшее и наименьшее значения этой функции на отрезке
. Вычислить наибольшее и наименьшее значения этой функции на отрезке 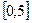 .
.
2) Найти интервалы монотонности и точки эксремума функции  . Вычислить наибольшее и наименьшее значения этой функции на отрезке
. Вычислить наибольшее и наименьшее значения этой функции на отрезке  .
.
3) Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
4) Написать уравнение касательной к кривой  в точке с абсциссой
в точке с абсциссой  .
.
ПЗ №9. Интегральное исчисление.
3. Разбор домашнего задания №6
4. Найти неопределенные интегралы:
 ; 2)
; 2) 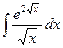 ; 3)
; 3)  ; 4)
; 4)  .
.
ПЗ№10. 5) Найти площадь фигуры, ограниченной линиями y2=9x и y=3x.
6) Найти площадь фигуры, ограниченной равнобочной гиперболой xy=4 и прямой x+y=5.
7) Определить длину половины окружности x2+y2=9.
ПЗ №11. Дифференциальные уравнения.
3. Разбор домашнего задания №10
4. Найти общее решение: 1) 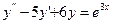 ; 2)
; 2) 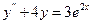 ; 3)
; 3) 
Решите задачу Коши: 1)  ;
;
2) 
ПЗ №12. Ряды. Числовые ряды.
3. Разбор домашнего задания №11
4. 1) Найти общий член ряда:  ;
;
2) Найти сумму ряда:  ;
;
3) Исследовать сходимость ряда:  ;
;
4) Исследовать сходимость ряда:  ;
;
5) Исследовать сходимость ряда:  .
.
ПЗ №13. Введение в теорию вероятностей.
3. Разбор домашнего задания №12
4. 1) Брошены две игральные кости. Найти вероятность того, что сумма очков на выпавших гранях равна семи.
2) В ящике содержится 10 одинаковых деталей, помеченных номерами 1, 2,..., 10. Наудачу извлечены 6 деталей. Найти вероятность того, что среди извлеченных деталей окажется деталь №1.
3) В цехе работают 7 мужчин и 3 женщины. По табельным номерам наудачу отобраны 3 человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
4) Вероятность успешной попытки выполнить упражнение для каждого из двух спортсменов равна 0,5. Спортсмены выполняют упражнение по очереди. Причем каждый делает по две попытки. Выполнивший упражнение первым получает приз. Найти вероятность получения приза спортсменами.
5) Отрезок АВ длиною 15 см разделен точкой С в отношении 2:1. На этот отрезок наудачу брошены 4 точки. Найти вероятность того, что две из них окажутся левее точки С и две-правее. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависист от его расположения.
6) Дискретная случайная величина Х задана законом распределения:
а) Х 2 4 5 6
Р 0,3 0,1 0,2 0,4
б) Х 10 15 20
Р 0,1 0,7 0,2.
Построить многоугольник распределения.
7) Найти математическое ожидание дискретной случайной величины Х, заданной законом распределения:
Х -4 6 10
р 0,2 0,3 0,5.
ПЗ №14. Теория вероятностей.
3. Разбор домашнего задания №13
4. 1) Двумерная случайная величина (X,Y) имеет плотность вероятности:  . Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми х=0, х=1, у=0, у=1.
. Найти вероятность попадания случайной точки в прямоугольник, ограниченный прямыми х=0, х=1, у=0, у=1.
2) Система двух случайных величин (X,Y) равномерно распределена в треугольнике, ограниченном прямыми у=х, у=5, х=5. Найти: а) МX, МY, DX, DY; б) коэффициент корреляции  .
.
3) Определить плотность вероятности ситемы двух положительных случайных величин X,Y по заданной функции распределения:  .
.
4) Случайные величины X и Y независимы и нормально распределены с MX=MY=0, DX=DY=25. Найти вероятность того, что случайная точка (X,Y) попадет в кольцо:  .
.
5) В механическом цехе работают К токарей. Вероятность того, что токарю потребуется резец данного типа, равна p. Сколько резцов данного типа должна иметь инструментальная кладовая, чтобы потребность в них была обеспечена с вероятностью 0,95?
6) Нарисуйте граф состояний для марковской цепи, вероятности перехода которой заданы матрицей  .
.
ПЗ №15. Математическая статистика.
3. Разбор домашнего задания №14
4. 1) Найти эмпирическую функцию по данному распределению выборки:
xi 1 4 6
ni 10 15 25.
2) Построить полигон частот по данному распределению выборки:
xi 1 4 5 7
ni 20 10 14 6.
3) Из генеральной совокупности извлечена выборка объема n=60:
варианта xi 1 3 6 26
частота ni 8 40 10 2.
Найти несмещенную оценку генеральной совокупности.
4) Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака Х генеральной совокупности, если даны генеральное среднее квадратичное отклонение σ=5, выборочная средняя 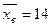 и объем выборки n=25.
и объем выборки n=25.
5) Найти коэффициент линейной корреляции между признаками Х и Y и написать уравнения прямых регрессии для корреляционной таблицы признаков:
| X/Y | Ni* | ||||||
| Nj* |
Контрольно-измерительные средства знаний (Вопросы для рубежного контроля)
17. Расстояние между двумя точками. Деление отрезка в данном отношении.
- Уравнение линии. Примеры составления уравнений данных линий. Построение линии по данному уравнению. Пересечение двух линий. Классификация линий.
- Различные способы задания прямой.
- Понятие о системе линейных уравнений с n не известными.
- Определители 2-го и n -го порядка, их свойства и вычисление.
- Правило Крамера и метод Гаусса для систем n линейных уравнений с n неизвестными.
- Матрица и ее ранг. Операции над матрицами. Матрица, обратная для данной и ее вычисление.
- Коллинеарные и компланарные векторы. Операции над векторами. Свойства суммы векторов. Единичный вектор. Основные теоремы о проекциях векторов на ось.
- Декартова прямоугольная система координат в пространстве. Разложение вектора по ортам.
- Операции над векторами, заданных в координатной форме. Скалярное произведение двух векторов и его свойства. Скалярное произведение векторов, заданных координатами. Угол между векторами. Условия коллинеарности и перпендикулярности векторов.
- Бесконечно малая и бесконечно большая последовательности. Понятие предела числовой последовательности. Ограниченность сходящихся последовательностей.
- Арифметические действия с пределами. Сходимость монотонных и ограниченных последовательностей.
- Понятие предела функции. Непрерывные функции.
- Определение производной. Геометрический смысл производной. Свойства производной. Производные основных элементарных функций.
- Определение дифференциала, связь с приращением. Свойства дифференциала. Применение дифференциала в приближенных вычислениях.
- Уравнение касательной к нормали к плоской кривой. Угол между двумя кривыми.
- Производные высших порядков. Механический смысл производной второго порядка.
- Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла.
- Таблица основных интегралов. Непосредственное интегрирование.
- Интегрирование путем замены переменной. Интегрирование по частям.
- Интегрирование некоторых выражений, содержащих квадратный трехчлен. Интегралы не выражающиеся через элементарные функции в конечном виде. Интегрирование рациональных функций.
- Интегрирование выражений, содержащие тригонометрические функции.
- Задачи, приводящие к понятию определенного интеграла. Свойства определенных интегралов.
- Связь между определенным и неопределенным интегралами. Применение определенного интеграла к вычислению площадей плоских фигур, площадей поверхностей вращения, длин дуг и объемов тел.
- Несобственные интегралы.
- Дифференциальные уравнения первого порядка и их решения. Геометрический смысл дифференциальные уравнения первого порядка.
- Дифференциальные уравнения с разделяющими переменными. Однородные уравнения первого порядка.
дифференциальным уравнениям.






