ПЗ№4. Составить уравнения всех сторон треугольника АВС, где А(3,2), В(5,-2) и С(5,2). Найти их длины.
5) Через точки А(1,-2) и В(5,4) проведена прямая. Составить уравнения прямых, проходящих через точку С(-2,0) перпендикулярно и параллельно прямой АВ. Вычислить растояние от точки С до прямой АВ.
6) Привести к каноническому виду уравнение кривой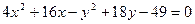 
. Определить ее тип, вычислить основные параметры.
7) Написать уравнение прямой, проходящей через точку М0(-1,2,1) и
а) имеющий направляющий вектор 
;
b) перпендикулярной плоскости 3x-y-2z+1=0;
с) проходящей через точку М0 и М1(3,2,4).
1. Расстояние d между двумя точками М1(х1) и М2(х2) координатной оси находится по формуле:
d = │х2 – х1│.
2. Расстояние d между двумя точками М1(х1,у1) и М2(х2,у2) плоскости находится по формуле:
d = √(х2 – х1)2 + (у2 – у1)2.
3. Расстояние d между двумя точками М1(х1,у1,z1) и М2 (х2,у2,z2) пространства находится по формуле:
d = √(х2 – х1)2 + (у2 – у1)2 + (z2 – z1)2.
4. Координаты (х,у) точки М, делящей отрезок с концами М1 (х1,у1) и М2 (х2,у2) в отношении λ, т.е. │М1М│: │ММ2│= λ, находится по формуле:
х1+λх2
х = ―――,
1 + λ
у1+λу2
у = ―――.
1 + λ
5. Координаты (х,у) точки М – середины отрезка с концами М1 (х1у1) и М2 (х2,у2) находятся по формуле:
х1+х2
х = ―――,
у1+у2
у = ―――.
6. Уравнение прямой:
- с угловым коэффициентом к и начальной ординатой b:
у = кх +b;
- проходящей в данном направлении (с угловым коэффициентом к) через данную точку М (х0, у0):
у – у1 = к (х1 - х1);
- проходящей через две данные точки М1 (х1,у1) и М2 (х2,у2):
у – у1 х – х1
―― = ――
у2 –у1 х2 – х1
у2 – у1
(с угловым коэффициентом к = ―――);
х2 – х1
- в отрезках:
х у
― + ― = 1
а b
(а и b – соответственно отрезки, отсекаемые на осях Ох и Оу);
- общее:
Ах + Ву +С = 0.
7. Расстояние d от точки А (х0,у0) до прямой Ах + Ву + С = 0 находится по формуле:
│Ах0 + Ву0 + С│
d = ―――――――.
√ А2 + В2
8. Две прямые (1) и (2) заданы уравнениями у = к1х +b1 и у = к2х +b2 или А1х + В1у + С1 = 0 и А2х + В2у + С2 = 0.
Угол φ между прямыми находится из соотношения:
←
к1 – к2
tg φ = ―――
1+к1к2
или
± (А1А2 + В1В2)
соs φ = ―――――――
√А12+В12 √А22+В22
Условие параллельности прямых:
А1 В1
к1 = к2 или ― = ―;
А2 В2
Условие перпендикулярности прямых:
к2 = - ― или А1А2 + В1В2 = 0
к1
Точка пересечения двух прямых находится из решения системы:
у = к1х +b1, А1х + В1у + С1 = 0,
или
у = к2х +b2, А2х + В2у + С2 = 0.
Кривые второго порядка
1. Общее уравнение кривых второго порядка:
Ах2+Вху+Су2+Еу+F=0
2. нормальное уравнение окружности радиуса Rс центром в точках С (х0,у0) и О (0,0) соответсвенно имеют вид:
(х-х0)2+(у-у0)2=R2
X2+y2 =R2
3. Каноническое уравнение эллипса:
х2/a2+y2/b2=1
а,b-оси эллипса: b2=a2-c2, F1(c;0) иF2(c;0)-фокусы эллипса.
Эксцентриситет эллипса ε=с/а
Расстояние точки М(х,у) эллипса до его фокусов:
r1=a-εx, r2=a+ εx.
4. Каноническое уравнение гиперболы
х2/a2-y2/b2=1
Расстояние точки М(х,у) гиперболы до фокусов:
r1=│a-εx│, r2=│a+ εx│
Уравнение обеих асимптот гиперболы у=±b/a x
5. Каноническое уравнение параболы с вершиной в начале координат:
У2=2рх
Расстояние от фокуса параболы F(p/2;0) до оси Ох(фокальный радиус):
R=x+p/2.
Уравнение диссектрисы параболы:
х=-р/2
6. Квадратный трехчлен у= Ах2 +Вх+С есть парабола с осью симметрии, параллельной оси Оу, и вершиной в точке (-В/2А,-D/4A), где D=В2 – 4АС—дискриминант.
