ПЗ №3. Элементы векторной алгебры и матричного анализа. Элементы аналитической геометрии.
1. Разбор домашнего задания №2
2. 1) Даны векторы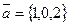 
и 
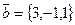. Найти косинус угла между векторам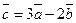и 
и 
.
2) При каком значении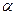 
векторы 
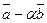и 
ортогональны (угол между ними равен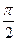 
)? Векторы 
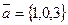и .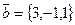
3) Вычислить угол между векторами 
и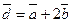 
, если 
, 
.
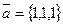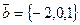3.1. Векторы на плоскости и в пространстве
1. Вектором называется направленный отрезок АВ с начальной точкой А и конечной точкой В (который можно перемещать параллельно самому себе).
Длиной (или модулем) |АВ| вектора АВ называется число, равное
длине отрезка АВ, изображающего вектор.
Векторы называются коллинеарными, если они лежат на одной прямой или параллельных прямых.
Векторы называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях.
2. Произведением вектора а на число λ называется вектор в= λа, имеющий длину |b| = |λ| |а |, направление которого совпадает с направлением вектора а, если λ> 0, и противоположно ему, если λ< 0.
Суммой двух векторов а и b называется вектор с =а + b, определяемый по правилу треугольника или параллелограмма.
Разностью двух векторов а и b называется вектор с = а + (-в).
3. Координатами (х, у) или (х, у, z) вектора а называются координаты его конечной точки, если начальная точка вектора совпадает с началом координат.
Вектор а = (х, у, z) может быть представлен в виде
а = xi + yj + zk
где i, j, k — единичные векторы (орты), совпадающие с направлением осей соответственно Ox, Oy, Oz; |i | = |j| =|k| = 1.
4. Длина | а | вектора а определяется по формуле:
| а | = х2+у2
или | а |= х2+у2+z2
5. Направляющими косинусами вектора а называются числа cos α, cos β, cos γ, где α, β, γ — углы наклона вектора а к осям Ох, Oy, Oz соответственно:
cos α=x/ x2+y2+z2, cos β=y/ x2+y2+z2, cos γ=z/ x2+y2+z2
при этом cos2 α + cos2 β + cos2 γ= 1.
6. Координаты суммы двух векторов а = (х1, у1, z1) и
b = (х2, у2,z2) и произведение вектора а на число λ определяются по формулам:
a + b =(х1, у1, z1)+(х2, у2,z2)= (xl+x2, y1+ y2, zl+z2), λа = λ(х1, у1, z1) = (λх1, λу1, λz1).
7. Проекцией пр а вектора а на ось I называется число
пр/ а = |a| cosφ, где φ — угол наклона вектора а к оси /.
8. Скалярным произведением (а, в) двух векторов а и в называется число
(а, b)=ab=|а| |b| cosφ
Скалярное произведение двух векторов а = (х1, у1, z1) и b= (х2, у2,z2) выражается формулой:
(а,b)=ab=xlx2+y1y2+z1z2.
Скалярный квадрат вектора а = (х,у,z) равен квадрату его длины:
(а,а)=а2 =|а|2 =x2+y2+z2.
9. Угол φ между векторами а = (х1, у1, z1) и b(х2, у2,z2) = находится по формуле:
cos φ=(а, b)/ |а| |b|= xlx2+y1y2+z1z2/ x12+y12+z12* x22+y22+z22.
10. Два вектора а, b называются ортогональными, если их скалярное произведение равно нулю, т. е. аb = 0.
11. Для двух векторов а = (х1, у1, z1) и b= (х2, у2,z2): условие коллинеарности (параллельности)
b=ka,или x2/x1=y2/y1=z2/z1=k
условие ортогональности (перпендикулярности)
аb = 0 или xlx2+y1y2+z1z2=0
