Вариант 1 4x2+z2+8xy+4xz Вариант 4 x2+2xy+2y2+2xz+4yz+3z2
Вариант 2 x2+3y2+4xy+2xz+2yz+z2 Вариант 5 x2+2y2+4xz+4yz
Вариант 3 ч2-н2+2чн+2чя
Задание 9
Приведите квадратичную форму к каноническому виду ортогональным
Преобразованием.
Вариант 1 -x2+2xy-y2
Вариант 2 4x2+4xy+8yz-3z2-4xz
Вариант 3 x2+y2+z2-4/3xz-8  yz
yz
Вариант 4 -x2-y2-3z2-2xy-6xz+6yz
Вариант 5 2x2+8xy+2y2+2z2+8xz-8y
Зачет №4
Математический анализ
1. Найти производные функций:
1) у = 4х5 – 2х3 + 3
2) y=2x 
3) y=x 
4) y= 
5) y=arctgx 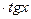
6) y= 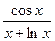
7) y=ln 
2. Написать уравнение касательной к кривой y=  в т. x =2
в т. x =2
3. Вычислить пределы:
1)  4)
4) 
2) 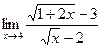 5)
5) 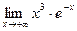
3) 
4. Найти интервалы выпуклости и точки перегиба графиков функции
1) у = х3 -6х2 +12х + 4
2) 
5. Исследовать функции и построить графики:
1) у = 3х – х3
2) 
Тезисы лекций
| № | Тема лекции | Тезисы лекции |
| Линейная алгебра с элементами аналитической геометрии. | Понятие о системе линейных уравнений с n не известными. Определители 2-го и n -го порядка, их свойства и вычисление. Правило Крамера и метод Гаусса для систем n линейных уравнений с n неизвестными. Матрица и ее ранг. Операции над матрицами. Матрица, обратная для данной и ее вычисление. | |
| Элементы векторной алгебры и матричного анализа. Элементы аналитической геометрии. | Коллинеарные и компланарные векторы. Операции над векторами. Свойства суммы векторов. Единичный вектор. Основные теоремы о проекциях векторов на ось. Декартова прямоугольная система координат в пространстве. Разложение вектора по ортам. Операции над векторами, заданных в координатной форме. Скалярное произведение двух векторов и его свойства. Скалярное произведение векторов, заданных координатами. Угол между векторами. Условия коллинеарности и перпендикулярности векторов. Расстояние между двумя точками. Деление отрезка в данном отношении. Уравнение линии. Примеры составления уравнений данных линий. Построение линии по данному уравнению. Пересечение двух линий. Классификация линий. Различные способы задания прямой. | |
| Введение в анализ. Пределы и непрер-ть. | Бесконечно малая и бесконечно большая последовательности. Понятие предела числовой последовательности. Ограниченность сходящихся последовательностей. Арифметические действия с пределами. Сходимость монотонных и ограниченных последовательностей. Понятие предела функции. Непрерывные функции. | |
| Дифференциальное исчисление функции одной переменной. Производная. Дифференциал функции. | Определение производной. Геометрический смысл производной. Свойства производной. Производные основных элементарных функций. Определение дифференциала, связь с приращением. Свойства дифференциала. Применение дифференциала в приближенных вычислениях. | |
| Приложение производной. Функции нескольких переменных. | Уравнение касательной к нормали к плоской кривой. Угол между двумя кривыми. Производные высших порядков. Механический смысл производной второго порядка. | |
| Интегральное исчисление. | Первообразная функция и неопределенный интеграл. Основные свойства неопределенного интеграла. Таблица основных интегралов. Непосредственное интегрирование. Интегрирование путем замены переменной. Интегрирование по частям. Интегрирование некоторых выражений, содержащих квадратный трехчлен. Интегралы не выражающиеся через элементарные функции в конечном виде. Интегрирование рациональных функций. Интегрирование выражений, содержащие тригонометрические функции.Задачи, приводящие к понятию определенного интеграла. Свойства определенных интегралов. Связь между определенным и неопределенным интегралами. Применение определенного интеграла к вычислению площадей плоских фигур, площадей поверхностей вращения, длин дуг и объемов тел. Несобственные интегралы. | |
| Дифференциальные уравнения. | Дифференциальные уравнения первого порядка и их решения. Геометрический смысл дифференциальные уравнения первого порядка. Дифференциальные уравнения с разделяющими переменными. Однородные уравнения первого порядка. Линейные уравнения первого порядка. Задачи, приводящие к дифференциальным уравнениям. | |
| Ряды. Числовые ряды. | Ряды. Сумма ряда. Признаки сходимости положительных рядов. Признак Даламбера. Интегральный признак Коши. | |
| Введение в теорию вероятностей. | Случайные события. Случайные величины. Функции распределения вероятностей. Дискретные и непрерывные распределения. Математическое ожидание и дисперсия. | |
| Теория вероятностей. | Одномерные и многомерные распределения. Предельные теоремы. Закон больших чисел. Цепь Маркова. | |
| Математическая статистика. | Понятия выборки, статистики и статистической оценки. Статистическое оценивание. Проверка статистических гипотез. | |
| Временные ряды. | Модели временных рядов и их составляющие. | |
| Классическая линейная модель множественной линейной регрессии. | Модель парной регресии. Св-ва коэффициентов регресии. Теорема Гаусса-Маркова. Формулы для коэффициентов и стандартных ошибок. Статистическая значимость коэффициентов линейной регрессии. | |
| Спецификация переменных. Мультиколлинеарность. Автокорреляция. Гетероскедастичность. | Влияние мультиколлинеарности на R2. Неэффективность МНК в случае гетероскедастичности. Автокорреляция первого порядка. Коэффициент детерминации. | |
| Нелинейные эконометрические модели. | Простейшие модели. Нелинейность по переменным и нелинейность по параметрам. Система одновременных уравнений. |






