График выполнения и сдачи СРСП

УЧЕБНАЯ ПРОГРАММА ДИСЦИПЛИНЫ

(syllabus)

Наименование дисциплины «Математика в экономике»

Специальность     Код дисциплины	5В050900- Финансы 5В050800 – Учет и аудит   ME-1202
Форма обучения	Дневная
Всего	3 кредита
Курс
Семестр
Лекции	30 часов
Практические, семинарские занятия	15 часов
Количество РК
СРСП	15 часов
СРС	60 часов
Экзамен	1 семестр
Трудоемкость	120 часов

 

 

А С Т А Н А – 2012

 

1. Сведения о преподавателе курса: Старший преподаватель каф. «Экономика и менеджмент» Карсыбаева Зауре Сабыровна, кабинет № 417.

Научные интересы преподавателя:

Мультипликаторы в весовых пространствах гладких функций и их приложения.

Владение языками: казахский - родной, русский - в совершенстве.

Данные кафедры: Кафедра Экономики и менеджмента, главный корпус КазГЮУ

2. Данные о дисциплине:

Математика для экономистов (3 кредита)

Выписка из учебного плана

Курс	Семестр	Кредиты	Лекции	Семинары	СРСП	СРС	Всего	Форма контроля
								экзамен

3. Пререквизиты:

Алгебра и начало анализа

Геометрия

Постреквизиты: 1.ЭММ; 2.Эконометрика; 3.Статистика; 4.Микроэкономика; 5.Макроэкономика; 6.Экономика.

Краткое описание дисциплины

Дисциплина «Математика для экономистов» ставит своей целью овладение студентами знаний по высшей математике в полном объеме, предусмотренном учебными планами КазГЮУ, которые понадобятся для обработки статистических данных. В результате осуществления данной цели у студентов формируется естественно- научный подход к изучению явлений повседневной жизни и навыки использования математических знаний в своей области деятельности.

Цель дисциплины

Целью математического образования является:

· воспитание достаточно высокой математической культуры;

· привитие навыков современных видов математического мышления;

· привитие навыков использования математических методов и основ математического моделирования в практической деятельности;

· формировать умения и навыки самостоятельного анализа исследования экономических проблем, развивать стремление к научному поиску путей совершенствования своей работы.

 

График выполнения и сдачи заданий по дисциплине

Виды работ	Цель и содержание задания	Рекомендуемая литература	Распределение часов	Баллы по шкале рейтинга	Форма контроля	Сроки сдачи
Подготовка к практическим занятиям с №1 по №15	Изложены в п. 2.3	В зави симости от темы практического занятия	1,0 час на подготовку к одному практическому занятию	2 балла за участие в практических занятиях	Решение задач по заданным темам	К практическим занятиям с №1 по №15
Домашние задания с №1 по №15	Изложены в п. 2.4	В зави симости от темы практического занятия	1,0 час на одно домашнее задание	3 балла за 15 домашних заданий	Сдача к практическому занятию с последующим обсуждением	К практическим занятиям с №1 по №15
Коллоквиум	Изложены в п.2.7	По темам лекций с №1 по №7	2 часа	30 баллов	Устный опрос по темам №1 по №17	К лекции №8 на 8-й неделе
Экзамен	Изложены в п. 2.8	По темам №1-15	2 часа	50 баллов	Письменные ответы	На 16-й неделе
Посещение занятий	Усвоение материала	По темам №1-15	90 часов	1 балл	Отметка в журнале	К каждому занятию

Введение

Совершенствование методов управления хозяйственной деятельностью в условиях рыночной экономики во многом связано с применением в экономической науке и практике разнообразных математических методов исследований. Математика стала для многих отраслей экономических знаний не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем.

Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую оставляющую в системе фундаментальной подготовки современного экономиста. По своей природе, экономика – самая близкая к математике социальная наука. Уже в определении самого понятия экономики, ее главных задач можно увидеть математические понятия и терминологию. Действительно, экономика – это общественная наука об использовании ограниченных ресурсов с целью максимального удовлетворения неограниченных материальных потребностей населения. Центральные проблемы экономической науки – рациональное ведение хозяйства, оптимальное распределение ограниченных ресурсов, изучение финансовых механизмов управления, разработка методов финансовых расчетов – по существу являются задачами, решаемыми в рамках математических наук. Количественные и качественные методы математики являются наилучшим вспомогательным аппаратом для получения ответов на следующие вопросы:

- что должно производиться (т.е. какие товары и услуги и в каком количестве надо производить)?

- как будут производиться товары (т.е. кем, с помощью какой технологии и каких ресурсов)?

- для кого предназначены эти товары (т.е. кем и как будут потребляться эти товары)?

Наконец, задача экономической теории, связанная с приведением в систему, истолкованием и обобщением поведения участников процесса производства, обмена и потребления, восходит к математическим проблемам оптимизации и принятия решения.

Математика нужна для того, чтобы с ее помощью исследовать сложные финансово-экономические проблемы.

Наиболее приспособленным, во многих случаях единственным и наилучшим, многофункциональным инструментом является математический аппарат.

С помощью математических методов исследуются сложные финансово-экономические задачи описательного, оптимизационного и управленческого типов, которые нельзя решить с помощью других более простых методов или основываясь только лишь на опыте и «здравом смысле».

Таким образом, можно говорить о следующих задачах, стоящих перед математикой в финансово-экономическом анализе:

· разработка математических моделей финансовых объектов;

· изучение условий существования оптимальных решений и их признаков;

· создание моделей планирования и прогнозирования;

· анализ экономических величин и статистических данных (эластичности, средних и предельных величин, регрессионный и корреляционный анализ и прогнозирование экономических факторов и показателей).

Любое ответственное решение в финансовом менеджменте требует проведения эксперимента. При наличии математической модели мы избавляемся от необходимости дорогостоящих экспериментов. Формализация позволяет сформулировать реальную задачу как математическую и позволяет воспользоваться для анализа универсальным и мощным математическим аппаратом, который не зависит от конкретной природы объекта. Математика проводит детальный количественный анализ модели, помогает предсказать поведение объекта и дает рекомендации для выбора наилучших вариантов решения проблемы.

В любой науке по тем или иным признакам можно выделить отдельные направления. Математика, возможно, как никакая другая наука, объединяет в себе большое количество предметов – от классической линейной алгебры и математического анализа до современной актуарной математики. При моделировании многих финансовых задач возникает необходимость учета случайных факторов и возмущений. В этом случае наиболее подходящим инструментом является аппарат теории вероятности.

Таким образом, многие математические дисциплины необходимы для применения непосредственно в финансово-экономических исследованиях в качестве инструментария.

Математика – наука о количественных отношениях и пространственнных формах действительного мира. В неразрывной связи с запросами науки и техники запас количественных отношений и пространственных форм, изучаемых математикой расширается, так что приведенное определение необходимо понимать в самом общем смысле.

В основе построения математической теории лежит аксиоматический метод, при котором в фундамент теории кладутся некотроые исходные положения, называемые аксиомами теории, а все остальные предложения теории получаются как логические следствия аксиом. Примером применения аксиоматического подхода является евклидова геометрия, в которой четко проведена идея получения основного содержания геометрической теории чисто дедуктивным путем из небльшего числа аксиом, истинность которых представлялась наглядно-очевидной.

Основным методом в математических исследованиях являются математические доказательства – строгие логические рассуждения. В силу объективной необходимости, указывает чл. - корр. РАН Л.Д. Кудрявцев, логические рассуждения представляют метод математики, без них математика немыслима. Следует отметить, что математическое мышление не сводится лишь к логическим рассуждениям. Для правильной постановки задачи, для оценки ее данных, для выделения из них существенных, для выбора способа ее решения необходима еще математическая интуиция, позволяющая предвидеть нужный результат прежде, чем он будет получен, наметить путь исследования с помощью правдоподобных рассуждений. Но справедливость рассматриваемого факта доказывается не проверкой ее на ряде примеров, не проведением ряда экспериментов (что само по себе играет большую роль в математических исследованиях), а часто логическим путем, по законам формальной логики.

Сказанное, естественно, не означает, что мы должны использовать только строгие доказательства, сводя ее к аксиомам. Такой задачи авторы не ставили потому, что это не только невозможно в рамках вузовского курса (а тем более краткого курса экономическом вуза), но часто и нецелесообразно с методической точки зрения. Так как в процессе изучения дисциплины в ограниченные сроки необходимо уделять большое внимание разъяснению математических понятий (в том числе и на интуитивном уровне), их геометрическому, физическому и экономическому смыслу, решению практических задач.

В математике изучаются математические модели. Это могут быть как непосредственно математические модели реальных явлений, так и объекты (структуры) для изучения этих моделей. Одна и та же математическая модель может описывать свойства далеких друг от друга по своему конкретному содержанию реальных явлений. Так, одно и тоже дифференциальное уравнение может описывать процессы роста населения и распада радиоактивного вещества. Для математики важна не природа рассматриваемых объектов, а существующие между ними отношения.

В математике используется два вида умозаключений: дедукция и индукция, позволяющие сделать выводы на основании частных случаев об общих суждениях. Принцип математической индукции гласит, что утверждение , зависящее от натурального параметра , считается доказанным для любого натурального числа , если доказано А(1) и для любого натурального числа из предположения, что верно , то доказано также .

При формулировке математических утверждений часто используется необходимые и достаточные условия. Пусть рассматривается какое-либо утверждение (положение В), в связи с некоторым утверждением (условием А). Если из В следует А, т.е. то А называется необходимым условием для В, если же из А следует В, т.е. 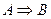, то А называется достаточным условием для В. Если одновременно верны утверждения и 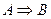, т.е. 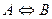, то А называется необходимым и достаточным условием для В. Например, для делимости числа на 6 необходимо достаточно, чтобы оно делилось на 2 и 3, ибо «делимость на 2 и 3 делимость на 6».

Таким образом, необходимые условия – те, без которых рассматриваемое утверждение заведомо не может быть верным, а достаточные условия – те, при выполнении которых это утверждение заведомо верно. Выражение «необходимо и достаточно» можно заменить равносильными выражениями «тогда и только тогда», «если и только если», «в том и только в том случае». Необходимые и достаточные условия обладают в математике большой познавательной ценностью.

Математика играет важную роль в естественнонаучных, инженерно-технических и гуманитарных исследованиях. Она стала для многих отраслей знаний не только орудием количественного расчета, но также методом точного исследования и средством предельно четкой формулировки понятий и проблем. Без современной математики с ее развитым и вычислительным аппаратом был бы невозможен прогресс в различных областях человеческой деятельности.

Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры. Поэтому математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки современного экономиста.

Содержание дисциплины

Тематический план лекций

№	Наименование темы	Количество часов
Лекции	Практ.зан.	СРСП	СРС
	Линейная алгебра с элементами аналитической геометрии.
	Система линейных уравнений.
	Векторный анализ.
	Уравнение линии на плоскости.
	Понятие функциональной зависимости.
	Понятие производной и дифференциала функции.
	Исследование функции.
	Функции нескольких переменных.
	Неопределенный интеграл.
	Определенный интеграл.
	Дифференциальные уравнения.
	Теория рядов. Числовые ряды.
	Степенные ряды.
	Теория вероятностей. Случайные события.
	Случайные величины и законы их распределения. Элементы математической статистики.
	ВСЕГО:

 

Тематический план семинарских занятий

№	Тема семинара	Краткое содержание семинара	Количество часов
	Матрицы и операции над ними.	Сложение и умножение матриц. Вычисление определителей. Обратная матрица.
	Система линейных уравнений.	Решение систем линейных алгебраических уравнений. Метод Крамера. Метод обратной матрицы. Метод Гаусса..
	Векторный анализ.	Сложение и умножение вектора на число. Скалярное умножение векторов. Ранг системы векторов. Разложение вектора по базису.
	Различные уравнения прямой и плоскости.	Уравнение прямой на плоскости. Кривые второго порядка. Прямая и плоскость в пространстве.
	Пределы и непрерывность.	Определение предела. Раскрытие неопределенностей различных типов. Замечательные пределы. Непрерывность функции и точки разрыва.
	Производная и дифференциал функции.	Основные теоремы диффеоенциального исчисления. Правило Лопиталя. Экстремумы функций. Асимптоты.
	Приложение производной.	Применеие дифференциального исчисления к исследованию функции и построе- ние их графиков. Применеие производной в задачах с экономическим содержанием.
	Функции нескольких переменных.	Производная по направлению. Градиент. Экстремум функции двух переменных. Функции нескольких переменных в экономических задачах.
	Неопределенный интеграл.	Табличные интегралы. Методы интегрирования неопределенного интеграла. Метод замены переменной. Метод интегрирования по частям.
	Определенный интеграл.	Методы вычисления определенного интеграла. Геометрические приложения определенного интеграла. Использование понятия определенного интеграла в экономике.
	Дифференциальные уравнения.	Основные понятия. Дифференциальные уравнеия первого порядка. Неполные дифференциальные уравнения первого порядка. Однородные дифференциальные уравнения. Линейные дифференциальные уравнения первого порядка. Линейные дифференциальные уравнеия второго пордка с постоянными коэффициентами.
	Числовые ряды.	Необходимые и достаточные условия сходимости числового ряда. Достаточные признаки сходимости знакоположительных рядов. Признак Даламбера и Коши. Знакопеременные ряды. Условная и абсолютная сходимость. Теорема Лейбница. Интегральный признак Коши.
	Элементы теории вероятностей.	Случайные события и их вероятности. Классификация событий. Теоремы сложения и умножения вероятностей
	Случайные величины.	Дискретные и непрерывные случайные величины и их законы распределения. Числовые характеристики случайных величин.
	Понятие многомерной случайной величины.	Функция распределения двумерной случайной величины. Закон распределения. Условные законы распределения. Числовые характеристики. Ковариация. Коэффициент ковариации.

Всего 15 часов.

 

График выполнения и сдачи СРСП

СРСП	Срок сдачи	Макс. оценка	Тема СРСП
СРСП № 1	1-2 неделя	3 балла	Сложение и умтожение матриц. Вычисление оптеделителей. Обратная матрица. Ранг матриц. Решение систем линейных алгебраических уравнений. Операции над векторами. Скалярное умножение векторов. Разложение вектора по базису. Уравнения прямой и плоскости. Предел функции. Непрерывность функции. Производная и дифференциал функции.   Применеие дифференциального исчисления к исследованию функции и построение их графиков.Производная по направлению. Градиент. Экстремум функции двух переменных. Неопределенный интеграл. Определенный интеграл. Дифференциальные уравнения. Необходимые и достаточные условия сходимости числового ряда. Теорема сложения и умножения вероятностей.   Повторные независимые испытания. Дискретные и непрерывные случайные величины и их законы распределения.   Закон распределения системы двух случайных величин.
СРСП № 2
СРСП № 3	3-4 неделя	3 балла
СРСП № 4
СРСП № 5	5-6 неделя	3 балла
СРСП № 6
СРСП № 7	7-8 неделя, 1- ый рубежный контроль	3 балла
СРСП № 8
СРСП № 9	9-10 неделя	3 балла
СРСП № 10
СРСП № 11	11-12 неделя	3 балла
СРСП № 12
СРСП № 13	13-14 неделя	3 балла
СРСП № 14
СРСП № 15	15 неделя, 2- ой рубежный контроль	3 балла