Ознаки мультиколінеарності

1. Якщо серед парних коефіцієнтів кореляції незалежних змінних є такі, рівень яких наближається або дорівнює множинному коефіцієнту кореляції, то це свідчить про можливість існування мультиколінеарності. Інформацію про парну залежність може дати симетрична матриця коефіцієнтів парної кореляції, або кореляції нульового порядку:

.

Але якщо в моделі фігурує більше двох незалежних змінних, вивчення питання про мультиколінеарність не може обмежуватись інформацією, що дає ця матриця. Явище мультиколінеарності ні в якому разі не зводиться тільки до існування парної кореляції між незалежними змінними.

Більш загальна перевірка передбачає визначення визначника (детермінанта) матриці r, який називається детермінантом кореляції і позначається . Числові значення детермінанта кореляції знаходяться на множині: .

2. Якщо , то існує повна мультиколінеарність, якщо — мультиколінеарність відсутня, чим ближче до нуля, тим певніше можна стверджувати, що між незалежними змінними існує мультиколінеарність. Незважаючи на те, що на числове значення впливає дисперсія незалежних змінних, цей показник можна вважати точковою мірою тісноти мультиколінеарності.

3. Якщо в економетричній моделі одержано мале значення параметра при високому рівні коефіцієнта детермінації і при цьому F -критерій суттєво відрізняється від нуля, то це також свідчить про наявність мультиколінеарності.

4. Якщо коефіцієнт детермінації , що розрахований для регресійних залежностей між однією незалежною змінною та іншими, має значення, яке близьке до одиниці, то можна говорити про наявність мультиколінеарності.

5. Якщо при побудові економетричної моделі на основі покрокової регресії включення нової незалежної змінної суттєво змінює оцінку параметрів моделі при незначному підвищенні (або зниженні) коефіцієнтів кореляції чи детермінації, то ця змінна, очевидно, знаходиться в лінійній залежності від інших, які введені в модель раніше.

Всі ці методи виявлення мультиколінеарності мають один загальний недолік: жоден із них не проводить чіткої межі між тим, що треба вважати «суттєвою» мультиколінеарністю, яку треба враховувати, і тим, коли мультиколінеарністю можна знехтувати.

Алгоритм Феррара—Глобера

Hайбільш повне дослідження мультиколінеарності можна здійснити на основі алгоритму Феррара—Глобера. Цей алгоритм включає три види статистичних критеріїв, на основі яких перевіряється мультиколінеарність всього масиву незалежних змінних (, хі-квадрат); кожної незалежної змінної зі всіма незалежними змінними (F -критерій) і мультиколінеарність кожної пари незалежних змінних (t -критерій).

Всі ці критерії при порівнянні з їх критичними значеннями дають можливість зробити конкретні висновки відносно наявності чи відсутності мультиколінеарності незалежних змінних.

Опишемо алгоритм Феррара—Глобера.

 

Крок 1. Стандартизація (нормалізація) змінних.

Позначимо вектори незалежних змінних економетричної моделі через . Елементи стандартизованих векторів розрахуємо за формулою:

де n — число спостережень, ;

m — число незалежних змінних, ;

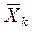— середня арифметична — її незалежної змінної;

— дисперсія -ї незалежної змінної.

Крок 2. Знаходження кореляційної матриці (матриці моментів стандартизо-

ваної системи нормальних рівнянь):

,

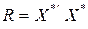де — матриця стандартизованих незалежних змінних;

— матриця, транспонована до матриці .

Крок 3. Визначення критерію (хі-квадрат):

,

де — визначник кореляційної матриці .

Значення цього критерію порівнюється з табличним при ступенях свободи і рівні значущості a. Якщо _{факт табл} , в масиві незалежних змінних не існує мультиколінеарності.

 

Крок 4. Визначення оберненої матриці (див.п.3):

.

 

Крок 5. Розрахунок F - критеріїв:

,

де c_kk — діагональні елементи матриці C. Фактичні значення критеріїв F_k порівнюються з табличними при і ступенях свободи і рівні значущості a. Якщо F_{k факт} > F_табл , відповідна k -та незалежна змінна мультиколінеарна з іншими.

Коефіцієнт детермінації для кожної змінної розраховується таким чином:

.

Крок 6. Знаходження часткових коефіцієнтів кореляції:

,

де c_kj — елемент матриці C, що заходиться в k -му рядку і j -му стовпці, , c_kk і с_jj — діагональні елементи матриці .

Крок 7. Розрахунок t критеріїв:

.

Фактичні значення критеріїв t_kj порівнюються з табличними при ступенях свободи і рівні значущості a. Якщо t_{kj факт} > t_табл, між незалежними змінними X_k і X_j існує мультиколінеарність.