Уравнение движения в напряжениях имеет вид:
. ( 4.39 )
Выберем цилиндрическую систему координат. Ось z направим по оси трубы, будем считать, что течение осесимметричное и 
, 
и 
. Действием массовых сил пренебрегаем.
Проекция уравнения (4.39) на ось z при сделанных предположениях будет иметь вид [4]:
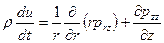. ( 4.40 )
Из уравнения неразрывности следует, что
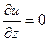. ( 4.41 )
Компоненты напряжений, учитывая (2.3) можно записать следующим образом
,
где 
, 
.
Уравнение (4.40) примет вид
. ( 4.42 )
Для степенных жидкостей
. ( 4.43 )
Для пульсирующего движения примем, что градиент давления запишется в виде
, ( 4.44 )
где 
- постоянная составляющая градиента давления.
Осциллирующая составляющая имеет амплитуду 
и частоту 
.
Пренебрегаем в уравнении (4.42) инерционным членом по сравнению с вязким и подставим (4.43) и (4.44) в (4.42), получим
. ( 4.45 )
При стационарном движении степенных жидкостей в трубах, при постоянном градиенте давления и с расходом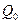 
мы ранее имели (3.26), что
. ( 4.46 )
Для пульсирующего движения из уравнения (4.45) легко получить, что
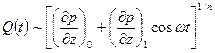. ( 4.47 )
Из (4.46) и (4.47) следует что,
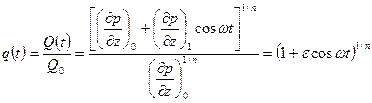, ( 4.48 )
где 
.
Обозначим через 
период колебания и введём безразмерное время 
, получим из (4.48)
. ( 4.49 )
Для среднего значения 
за период колебания будем иметь
. ( 4.50 )
Величина 
показывает отношение среднего за период колебания расхода при пульсирующем движении к расходу при постоянном перепаде давления.
Результаты расчётов по формуле (4.50) при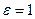 
представляются в таблице:
| n | 0,4 | 0,7 | 1,0 | 1,4 |
|
| 1,9 | 1,17 | 1,0 | 0,97 |
Итак, мы получили, что наложение пульсаций на течение в трубе приводит к увеличению расхода для псевдопластичных жидкостей и к его уменьшению для дилатантных [16].
Найдём мощность, теряемую жидкостью на единицу длины трубы:
. ( 4.51 )
Из (4.48) и (4.44)
. ( 4.52 )
. ( 4.53 )
Подставив в (4.52) и (4.53) в (4.51), получим
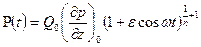. ( 4.54 )
Мощность, теряемая жидкостью за период колебания на единицу длины трубы
. ( 4.55 )
При стационарном движении с расходом 
(средним значением за период колебания) имеем
, ( 4.56 )
где 
- градиент давления, обеспечивающий расход .
При стационарном движении с расходом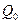
. ( 4.57 )
При стационарном движении степенной жидкости в трубе имеем
, 
( 4.58 )
Из (4.58) 
или
. ( 4.59 )
Обозначив 
, получим из (4.55), (4.56) и (4.59), учитывая, что
. ( 4.60 )
Значения рассчитываются по формуле (4.50).
Результаты расчётов по формулам (4.50) и (4.60) при 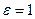представлены ниже в таблице
| n |
| P |
| 0,7 | 1,17 | 1,43 |
| 1,0 | 1,0 | 1,50 |
| 1,4 | 0,97 | 1,58 |
Получено, что при пульсациях давления в трубах средний за период колебания расход увеличивается для псевдопластичных жидкостей и уменьшается для дилатантных. Для ньютоновских вязких жидкостей наложение пульсаций не влияет на расход. Мощность, затрачиваемая на движение жидкости при пульсирующем течении для всех типов вязких жидкостей, увеличивается при том же значении расхода. Следует напомнить, что полученные результаты верны в случае, когда инерционные члены малы по сравнению с вязкими.
Глава V
