Дадим теперь полное решение задачи об установившемся пограничном слое на абсолютно гладкой тонкой неподвижной пластинке – полуплоскости 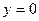
 (см. рис. 5.1), когда скорость
(см. рис. 5.1), когда скорость  набегающего потока постоянна и направлена по оси x (по пластинке).
набегающего потока постоянна и направлена по оси x (по пластинке).
В этом случае уравнения (5.8) и (5.3) приобретают вид

 ,
,
(5.12)
 ,
,
так как движение установившееся, а внешний поток представляет собой поступательное движение с постоянным давлением  .
.
На пластинке имеем условие прилипания
при
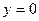 ,
, 
 , (5.13)
, (5.13)
на внешней границе пограничного слоя
при

 . (5.14)
. (5.14)
Так как в рассматриваемой задаче нет характерного линейного размера, то система размерных и безразмерных определяющих параметров имеет вид
 ,
, 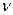 ,
,  ,
,  и
и  ,
,  . (5.15)
. (5.15)
Поэтому искомые функции  и
и  можно представить через безразмерные функции
можно представить через безразмерные функции 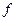 и
и  вида:
вида:
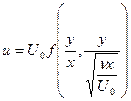 ,
, 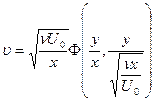 . (5.16)
. (5.16)
Если теперь в уравнениях (5.12) и в граничных условиях (5.13) и (5.14) совершить замену переменных:
 ,
,  ,
,  ,
,  , (5.17)
, (5.17)
то получим

 ,
,
 (5.18)
(5.18)
при  ,
, 

 ,
,
при 

 .
.
Уравнения и граничные условия для функций  и
и 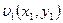 не содержат параметра
не содержат параметра  , поэтому решение системы (5.18) не должно зависеть от
, поэтому решение системы (5.18) не должно зависеть от  . Из (5.16) получим:
. Из (5.16) получим:

 ,
,
(5.19)
 ,
,
так как аргумент  содержит параметр
содержит параметр  , от которого решение не зависит.
, от которого решение не зависит.
Из формул (5.19) вытекает, что уравнения с частными производными (5.18) приводятся в данной задаче к обыкновенным уравнениям с одной независимой переменной
 . (5.20)
. (5.20)
Решение задачи Блязиуса
В общем случае из уравнения неразрывности

следует, что для плоскопараллельных движений несжимаемой жидкости существует функция тока  такая, что
такая, что
 и
и  .
.
Полагая
 ,
,
найдём
 .
.
Таким образом, на основании уравнения неразрывности получим, что компоненты  и
и 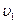 выражаются через функцию
выражаются через функцию 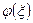 в виде
в виде

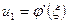 ,
,
 . (5.21)
. (5.21)
Подставляя (5.21) в уравнение движения, после простых преобразований получим
 . (5.22)
. (5.22)
Для получения решения этого нелинейного обыкновенного дифференциального уравнения третьего порядка необходимо найти функцию 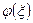 в интервале
в интервале  , удовлетворяющую уравнениям (5.22) и на концах интервала
, удовлетворяющую уравнениям (5.22) и на концах интервала  следующим граничным условиям, вытекающим из (5.18):
следующим граничным условиям, вытекающим из (5.18):
 и
и  . (5.23)
. (5.23)
Для определения функции 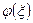 требуется решить краевую задачу. Эту краевую задачу легко свести к задаче Коши с данными на одном конце, если воспользоваться следующим общим свойством решений уравнения (5.22).
требуется решить краевую задачу. Эту краевую задачу легко свести к задаче Коши с данными на одном конце, если воспользоваться следующим общим свойством решений уравнения (5.22).
Пусть  - некоторое решение уравнения (5.22); непосредственной проверкой легко убедиться, что функция
- некоторое решение уравнения (5.22); непосредственной проверкой легко убедиться, что функция
 (5.24)
(5.24)
также является решением уравнения (5.22) при любом постоянном  .
.
Определим теперь функцию  как решение следующей задачи Коши для уравнения (5.22):
как решение следующей задачи Коши для уравнения (5.22):
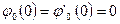 ,
,  . (5.25)
. (5.25)
С помощью уравнения (5.22) и данных Коши (5.25) функцию  нетрудно рассчитать известными численными методами для любых
нетрудно рассчитать известными численными методами для любых  . По данным расчёта можно определить предел
. По данным расчёта можно определить предел
 , причём
, причём  . (5.26)
. (5.26)
Определим теперь в формуле (5.24) постоянную  таким образом, чтобы удовлетворялось условие (5.23) при
таким образом, чтобы удовлетворялось условие (5.23) при  . Имеем:
. Имеем:
 ,
, 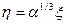
и
 ,
,  .
.
Отсюда следует, что
 .
.
Очевидно, что для получения искомого решения для функции 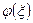 с помощью формулы (5.24) достаточно положить
с помощью формулы (5.24) достаточно положить  или на основании (5.26)
или на основании (5.26)
 .
.
Следовательно, полное решение представляется формулами (5.21) и (5.24) при  , определённой из численного решения задачи Коши (5.25).
, определённой из численного решения задачи Коши (5.25).
Сопротивление трения
Вычислим теперь касательную составляющую  напряжения вязкого трения на поверхности пластинки. Имеем
напряжения вязкого трения на поверхности пластинки. Имеем
 . (5.27)
. (5.27)
Напряжение трения зависит от координаты x и падает с ростом x.
Полное сопротивление одной стороны прямоугольного участка пластинки шириной b и длины по потоку L представится формулой
 .
.
Отсюда для коэффициента трения получим
 (5.28)
(5.28)
где  .
.
Таким образом, в этом случае полное сопротивление пропорционально скорости обтекания U0 в степени  , а коэффициент трения обратно пропорционален корню квадратному из числа Рейнольдса.
, а коэффициент трения обратно пропорционален корню квадратному из числа Рейнольдса.
Напомним, что сила сопротивления движению тел с постоянной поступательной скоростью в вязкой жидкости при малых числах Рейнольдса пропорциональна первой степени скорости.






