Технически важным примером течения с преобладающей ролью вязкости может служить течение в тонком смазочном слое при относительном движении двух твердых тел, разделенных этим слоем.
Закономерности движения такого тонкого вязкого слоя составляют содержание гидродинамической теории смазки, основы которой были заложены трудами О. Рейнольдса, Н.П. Петрова, Н.Е. Жуковского, С.А. Чаплыгина.
Такое течение обладает замечательным свойством: разности давлений в нем могут достигать очень больших значений, вследствие чего тонкий слой масла, находящийся, например, между валом и подшипником, поддерживает вал, предохраняя его от непосредственного соприкосновения с подшипником. Наиболее существенные особенности течения масла в смазочном слое можно выяснить на примере ползуна и плоской опорной поверхности, образующих друг с другом малый угол (рис.4.1.). Решение этой задачи было выполнено О. Рейнольдсом [3], [5].
Рассмотрим плоский случай 
зададим (рис.4.1.) отрезком CD опорную плоскость ползуна, а отрезок ОВрасположим плоскости, вдоль которой ползун движется (отрезок ОВравен проекции CD на эту плоскость). Угол между CD и ОВ считается малым, так же как и среднее расстояние между этими плоскостями в интервале ОВ.
Предполагая перемещение ползуна поступательным, прямолинейным и равномерным со скоростью U, параллельной ОВ, обратим движение, сообщив рисунку такую же скорость в противоположном направлении. Ползун при этом представится неподвижным, а отрезок ОВбудет двигаться в плоскости со скоростью U в направлении от широкой части щели BD кузкой ОС. По свойству прилипания вязкой жидкости к твердой поверхности она будет увлекаться в том же направлении.
Обозначим через 
и 
соответственно высоты выходного и входного сечений щели, h — текущую ординату отрезка CD, а —проекцию CD на ось Ох, направленную вдоль ОВ, как это показано на рисунке. Уравнение отрезка CD зададим формулой
(4.20)
где k — постоянный коэффициент, равный
(4.21)
Заметим, что (штрих означает производную по х)
(4.22)
При составлении уравнений движения вязкой жидкости, увлекаемой в клинообразную щель движущимся отрезком ОВ, примем во внимание тонкость щели и непроницаемость стенок, ограничивающих щель. Это позволит считать поперечную скорость Vy пренебрежимо малой по сравнению с Vх, а производную 
значительно большей, чем 
. Пренебрегая, кроме того, конвективными членами, приведем систему уравнений Навье – Стокса к виду
(4.23)
Граничные условия будут:
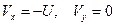при 
при 
(4.24)
при 
и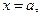 
причем последнее условие соответствует выравниванию давления вне вязкого клина.
Интегрируя обе части первого уравнения системы (4.23) по у и принимая во внимание граничные условия (4.24), получим
(4.25)
Условие одинаковости расходажидкости сквозь любое сечение потока дает
или, после подстановки Vx из (4.25) и интегрирования,
Судя по последнему граничному условию системы (4.24), в промежуточной точке с абсциссой хт в интервале 0 < хт < a должно выполняться условие dp/dx = 0. Вводя обозначение h = hm при х = хт, из предыдущего равенства найдем
Исключая константу, из последних двух уравнений получим
откуда следует
(4.26)
Вычислив в точке х=хт производную 
убедимся в том, что в силу условия (4.22) она имеет отрицательное значение. Отсюда следует, что в точке х=хт давление максимально.
Перейдем от аргумента х к h, используя для этого основное геометрическое соотношение (4.20), согласно которому
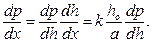
Перепишем после этого равенство (4.26) в форме
(4.27)
и проинтегрируем его по h, будем иметь
(4.28)
Используя граничные условия (4.24) и равенство (4.20), найдем постоянные интегрирования hm и b:
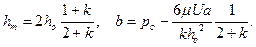(4.29)
Подставляя эти значения постоянных в (4.28) и возвращаясь к переменной х, получим следующее окончательное выражение для р(х):
(4.30)
причем абсцисса хт, как это непосредственно следует из (4.20) и первого равенства системы (4.29), будет равна
(4.31)
Решим теперь основной вопрос о величине направленной вдоль Oy силы R, поддерживающей ползун. Имеем по (4.30) (над CD давление равно po)
(4.32)
Обратим внимание на то, что сила R, поддерживающая ползун, обратно пропорциональна квадрату малой величины ho. Поэтому при возрастании нагрузки, прижимающей верхнюю пластинку к нижней, и прочих постоянных параметрах уменьшается зазор ho и возрастает сила R до значения, уравновешивающего нагрузку. Таким образом, смазочный слой не выдавливается и может выдерживать весьма значительные нагрузки. Необходимо подчеркнуть, что основную роль в этом явлении играет наклонное положение обеих стенок друг относительно друга, то есть эффект «вязкого клина».
Сила R достигает своего максимума при 
то есть при 
, и равна при этом
(4.33)
Для определения сопротивления F движению ползуна найдем сначала напряжение трения τ на его опорной поверхности или, что все равно, в силу малости угла раствора клинообразной щели, на отрезке ОВ
откуда, согласно (4.25)
и, после подстановки значения dp/dx по (4.26) и h по (4.20)
(4.34)
Интегрируя по x от x = 0 до х=а, определим полную силу сопротивления движению ползуна
(4.35)
При k= 1,2, соответствующем максимальной поддерживающей силе, будет
(4.36)
Коэффициент трения, условно определяемый отношением величины сопротивления к величине поддерживающей силы, как видно из формул (4.35) и (4.32), пропорционален ho /a, т. е. очень мал.
Проиллюстрируем основной факт достижения больших поддерживающих сил ползуна за счет малостизазора между опорной поверхностью ползуна и плоскостью его скольжения. При оптимальном значении отношения 
рассмотрим случай квадратного в плане ползуна, а = 0,1 м, ho=10-4 м, U = 1 м/с, µ = 0,706·10-1 Н·с/м2.
Расчет по формуле (4.33) показывает, что в этих условиях Rmax достигает значения 1130 Н. Это делает понятным существование больших поддерживающих сил в обильно смазанных подшипниках скольжения и указывает на главную причину образования таких сил – эффект «вязкого клина».
Найдем абсциссу хR точки приложения равнодействующей R распределенных по отрезку CD элементарных поддерживающих сил. С этой целью составим момент равнодействующей Lc как интеграл (малость раствора «клина» позволяет принять косинус этого угла равным единице)
(4.37)
после чего абсцисса xR определится как 
, то есть согласно (4.32) и (4.37), будет равна
(4.38)
При k = 1,2 будет xR≈0,42 а, то есть точка приложения поддерживающей силы R находится не посередине несущей поверхности (отрезка CD), а несколько ближе к точке С, что объясняется значительным сдвигом точки максимума давления (
) к левому краю ползуна.
