Рассмотрим задачу об установившемся обтекании шара потоком ньютоновской жидкости, имеющим на бесконечности постоянную скорость Uo при давлении 
.
Решение этой задачи при малых числах Рейнольдса принадлежит Стоксу. Подробное изложение метода получения решения приведено в 
.
Совместим центр шара с началом координат и направим ось х параллельно скорости U 0, радиус шара пусть равен R. Система уравнений (4.2) и (4.3) имеет вид
, 
, 
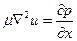. (4.10)
Граничные условия:
, 
, где 
, 
, 
, 
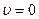. (4.11)
В постановке Стокса характеристики потока зависят только от следующих параметров: 
µ, R, U0.
Сила сопротивления шара F может выражаться только через эти величины; из них можно составить одну комбинацию с размерностью силы – произведение µ·R·U0. Следовательно, пользуясь теорией размерности получим:
, (4.12)
где с – постоянная величина.
Не входя в подробности вычислений, приведем решение системы уравнений (4.10) с граничными условиями (4.11). Получим следующие формулы для составляющих скорости и давления:
(4.13)
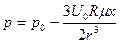
где 
.
Полное сопротивление шара F можно получить, используя полученное решение. Получим
. (4.14)
Это есть известная формула Стокса для сопротивления шара. Необходимо отметить, что сопротивление пропорционально первой степени скорости. Сравнив (4.14) и (4.12) получим, что с=6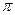 
.
Полученное решение соответствует действительности только при малых значениях числа Рейнольдса 
<<1, где d=2R.
Представим сопротивление F как произведение коэффициента сопротивления сх на площадь 
поперечного сечения шара и на динамическое давление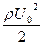 
. Получим
. (4.15)
Заменив F его значением из формулы (4.14), найдем коэффициент сопротивления
(4.16)
где .
Полученное выше решение задачи об обтекании шара было уточнено Осееном. Дело в том, что на достаточно больших расстояниях от шара решение Стокса оказывается неприемлемым. Для того, чтобы убедиться в этом, оценим член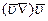 
, которым мы пренебрегли в уравнении (4.1). Для такой оценки обратимся к соотношениям (4.13) и рассмотрим для простоты только точки, лежащие на оси Ох, для которых х = r. На больших расстояниях 
. Производные же от скорости на этих расстояниях порядка величины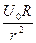 
, как это видно из (4.13). Следовательно, 
. Оставленные же в уравнении (4.1) члены – порядка величины 
(как это видно из (4.13) той же формулы для скорости или для давления). Условие >> 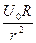выполняется только на расстояниях 
<< 
(
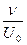<<1). На больших расстояниях полученное распределение скоростей оказывается неправильным [2].
Для получения распределения скоростей на больших расстояниях от обтекаемого шара следует учесть отброшенный в (4.1) член 
. Так как на этих расстояниях скорость 
мало отличается от U0, то можно написать приближенно 
вместо 
. Тогда мы получим для скорости на больших расстояниях линейное уравнение
. (4.17)
Решение этого уравнения изложено в 
. С помощью этого решения можно получить уточненную формулу для коэффициента сопротивления шара:
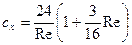. (4.18)
Результаты опытов показывают, что формула Осеена (4.18) пригодна до Re = 1,5. Уточнение Осеена оправдано вдали от шара на расстояниях r>>R. Поэтому, давая правильное уточнение картин движения на больших расстояниях от обтекаемого тела, уравнение Осеена не дает такого уточнения на близких расстояниях. Это проявляется в том, что решение Осеена не удовлетворяет точному условию обращения в нуль скорости на поверхности шара. Поэтому может показаться, что поправка Осеена не может послужить для правильного вычисления поправочного члена в силе сопротивления. Однако, поскольку мы рассматриваем движения с малыми числами Re, то как полные инерционные члены, так и заменяющие их поправочные выражения Осеена в уравнении (4.17) будут малы по сравнению с членами, происходящими от сил вязкости. Следовательно, в области, примыкающей к шару уравнения (4.17) и уравнения Стокса (4.10) являются в одинаковой мере хорошими приближениями к полной системе дифференциальных уравнений (4.1).
Формулу Стокса (4.14) или (4.16) можно применять только в случаях очень малых чисел Рейнольдса, например для дождевых капель или пыли в атмосфере, падения стальных шариков в очень вязких жидкостях.
Пользуясь формулой Стокса (4.14) при очень малых числах Re можно найти скорость осаждения мелких капель тумана и прочих мелких частиц. Приравнивая силу сопротивления шара (4.14) результирующей сил гидростатического давления, получим формулу для скорости падения шариков малых размеров в вязкой жидкости.
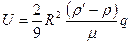(4.19)
где 
- плотность вещества шарика, 
- плотность жидкости.
Формула (4.19) используется для определения коэффициента вязкости сильно вязких ньютоновских жидкостей. Вискозиметр, основанный на принципе падения тяжелого шарика, состоит из трубки с делениями. Время падения от одного фиксированного деления трубки до другого, определяется секундомером. Найденное так значение скорости подставляют в (4.19) и определяют коэффициент динамической вязкости. При больших числах Рейнольдса полученные выше формулы становятся неудовлетворительными. Объясняется это тем, что с возрастанием числа Рейнольдса в кормовой области шара образуется отрыв и сложные нестационарные явления типа автоколебаний. Для широкого диапазона чисел Re приходится пользоваться эмпирическими данными или решать задачу численно.
