Рассмотрим решение задачи Блязиуса о пограничном слое в несжимаемой жидкости вдоль плоской пластинки приближенным методом, используя интегральное соотношение Кармана [4]. Так как мы имеем дело с установившимся движением, в котором
то уравнение (5.47) напишется так:
(5.48)
Если бы нам было известно, что распределение скорости внутри пограничного слоя определяется формулой
,
где
то мы имели бы
где для краткости введено обозначение
(5.49)
Далее,
(5.50)
поэтому уравнение (5.48) принимает вид:
откуда
Интегрируя это уравнение и считая, что δ = 0 при х = 0, получим:
(5.51)
Так как вследствие формул (5.50) и (5.51):
то для сопротивления, испытываемого с одной стороны пластинкой ширины b и длины L, мы получим формулу
, (5.52)
для коэффициента трения имеем:
(5.53)
Наконец, для определения величины δ* мы имеем, согласно формуле (5.31):
(5.54)
Основная идея метода Кармана состоит в том, что вместо того чтобы отыскивать точный вид функции f(η), можно задать вид этой функции. Если мы правильно схватим общий характер распределения скоростей в пограничном слое, то получим хорошее приближение как для зависимости δ от х, так и для численной величины коэффициента сопротивления.
Отсюда видны и положительные и отрицательные стороны метода Кармана. Этот метод хорош тем, что он требует гораздо меньших вычислений по сравнению с точными методами интегрирования дифференциальных уравнений теории пограничного слоя. Плохая же сторона метода Кармана состоит в том, что он применим только к тем случаям, когда мы имеем плавное распределение скорости в пограничном слое, так как только в этих случаях мы можем ожидать, что задаваемая с довольно большим произволом функция f(η) отразит общий характер течения в пограничном слое. Поэтому, в сущности говоря, мы должны довольно много знать о характере течения в пограничном слое, чтобы иметь возможность применять метод Кармана.
В нашей задаче мы имеем дело с очень плавным распределением скоростей, и поэтому мы должны ожидать, что метод Кармана даст хорошие результаты. В самом деле, примем, например, что
(5.55)
это обеспечивает нам при y = 0 u = 0, а при y = δ u = U0, как и должно быть. Мы будем тогда иметь:
поэтому формула (5.51) дает:
(5.56)
а по формулам (5.52) и (5.53)
(5.57)
Наконец для δ* имеем формулу:
(5.58)
Возьмем теперь распределение скоростей по параболе третьей степени
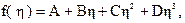
причем выберем следующие граничные условия:
u = 0, 
при y = 0; u = U0, 
при y = δ, (5.59)
последнее из которых выражает, что на внешней границе пограничного слоя не только u, но и 
плавно переходят в соответствующие значения внешнего потенциального течения. Второе из взятых нами пограничных условий сразу вытекает из уравнения (5.59), если заметить, что при y = 0 как uх, так и υ должны обращаться в нуль. Простое вычисление показывает, что надо взять
(5.60)
и далее
следовательно,
(5.61)
Мы видим, что величина d* во всех случаях получается очень близкой к той, которую дает точное решение; ошибка в определении сf доходит до 15%, хотя в случае, когда за f(h) выбирают полином третьей степени эта ошибка не превышает 3%.
