Свойство газа занимать весь объём сосуда, в котором он находится, тоже возникает из-за стремления молекул газа к беспорядку. Если сначала разместить все молекулы газа в какой-то малой части сосуда, а потом снять ограничения, разрешив им двигаться, то они равномерно заполнят весь его объём. вероятность того, что молекулы опять соберутся все вместе в той части сосуда, где они были сначала, ничтожно мала. Поэтому и этот процесс расширения газа тоже необратим.
второй закон термодинамики: если замкнутая система из макроскопических тел переходит в другое состояние, то этот переход необратим, т.к. он всегда происходит из менее вероятного состояния в более вероятное.
Р. Клаузис: теплообмен в замкнутой системе может происходить только в одном направлении – от горячего тела к холодному.
№61 Цикл Карно. Для работы теплового двигателя необходимо наличие 2-ух резервуаров: нагревателя и холодильника. Предположим что теплоемкость двигателя велика, поэтому температура при обмене теплоты не меняется. Цикл состоит из 2-ух изотрем(единственный обратимый процесс, при котором температура резервуаров при котором остается постоянной.) и 2-ух адиабат. Цикл обратимый. Вывод КПД. Количество теплоты системы при обратимом процессе: 
. Цикл совершает обратимый процесс, т.е. изменение энтропии нулю. При 1-ой изотерме приращение энтропии 
. При второй изотерме идет отнятие тепла у тела 
. Полное приращение равно нулю. 
; 
; 
.
№62 Энтропия. Закон возрастания энтропии. Вывод Макросостояние характеризуется каким-то микросостоянием, т.е. статистическим весом 
. Для доказательства ее аддитивности(разбиения на неограниченное количество частей с сохранение характеристик первоначального) разобьем на 2 невзаимодейсвующие системы 
1 и 2. Общий статистический вес равен произведению отдельных, т.е. = 1* 2. Возьмем логарифм от этого выражения ln = 
1+ 2. ln -аддитивная величина, ее можно разбить на части. В качестве характеристики состояния берется величина S=k*ln . Это энтропия. Её свойства: 1) Энтропия при протекании необратимого процесса возрастает(изолированная система переходит из менне вероятных состояний в более.) 2)Энтропия системы, находящееся в равновесном состоянии максимальна. 1-ое свойство есть закон возрастания энтропии или второе начало термодинамики.
№63 Фазовые переходы. Формула Клайперона-Клаузиса. Критическая точка. Фазовый переход — переход вещества из одной фазы в другую при изменении внешних условий.(фаза-совокупоность однородных и одинаковых по своим свойствам частей системы, например вода и пар в закрытом сосуде).Фазовый переход происходит, когда система пересекает линию, разделяющую две фазы на графике. Наиболее распространённые примеры фазовых переходов первого рода: плавление и кристализация, испарение и конденсация, сумблимация и десумблимация. Критическая точка -это сочетание значений температуры и давления, в которой различия между газообразным и жидким фазами полностью стираются, т.е. все характеристика(плотность и т.д.) индетичны. Пример: (критическая точка для 2-ух фаз: пара и воды, температура в 100, при нормальном давлении). Вывод Клайперона-Клаузиса: В цикле Карно при различии температур холодильника и нагрев на 
(б.м.в.) и dP(б.м.в.) формула для расчета КПД: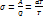 
; А=P(V2-V1)-(P-dP)(V2-V1)=M(
1- 
dP. (
, M-масса).q-удельная теплота фазового перехода равна 
. Подставим полученный выражения в формулу кпд: 
или 
.
№64 Реальные газы. Уравнение Ван-Дер-Вальса Реальный газ — газ, который не описывается уравнением состояния идеального газа Клапейрона — Менделеева. Зависимости между его параметрами показывают, что молекулы в реальном газе взаимодействуют между собой и занимают определенный объём. уравнения состояния реального газа описывается уравнением Ван-дер-Ваальса. Для более точного описания поведения реальных газов при низких температурах была создана модель газа Ван-дер-Ваальса, учитывающая силы межмолекулярного взаимодействия. В этой модели внутренняя энергия 
становится функцией не только температуры, но и объёма. Для одного моля газа Ван-дер-Ваальса оно имеет вид: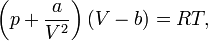 
учитывает силы притяжения между молекулами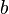 
— силы отталкивания (из общего объёма вычитаем объём, занимаемый молекулами). Для 
молей газа Ван-дер-Ваальса уравнение состояния выглядит так: 
Внутренняя энергия Ван-дер-Ваальса для одного моль газа: 
.Где 
— молярная теплоёмкость при постоянном объёме, которая предполагается не зависящей
