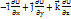Всякая система, которая движется с ускорением по отношению к инерциальной системе отсчета, является неинерциальной. Практически удобно пользоваться системами координат, которые имеют ускорение по отношению к Солнцу и звездам, например, системой координат, связанной с Землей. В таких неинерциальных системах координат механика Ньютона уже не справедлива. Как происходит движение по отношению к вращающейся СО и какие здесь появляются силы. Такой СО является Земля(суточное вращение). Благодаря небольшой скорости вращения эти силы невелики, но легко обнаруживаются. Для простоты представим, что СО является равномерно вращающийся диск и рассмотрим простейшее движение на нем (равномерно движущуюся по краю частицу). Обозначим скорость относительно диска vн (прим. н – неинерциальная СО). Скорость этой же частицы относительно неподвижного наблюдателя (ин. СО) – vи = vн + ΩR. Легко определить теперь ускорение частицы по отношению к инерциальной СО, т.к. частица равномерно движется по окружности радиуса R со скоростью vи. 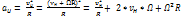 (1). Если это ускорение умножить на массу частицы m, то найдем силу, действующую на частицу в инерциальной СО F=maи. Посмотрим теперь как будет рассматривать это движение наблюдатель, находящийся на диске и считающий его неподвижным. Для него частица также движется по окружности радиуса R, но её скорость = vн. Поэтому ускорение частицы относительно диска будет aн =
(1). Если это ускорение умножить на массу частицы m, то найдем силу, действующую на частицу в инерциальной СО F=maи. Посмотрим теперь как будет рассматривать это движение наблюдатель, находящийся на диске и считающий его неподвижным. Для него частица также движется по окружности радиуса R, но её скорость = vн. Поэтому ускорение частицы относительно диска будет aн =  и направлено к центру диска. Считая диск неподвижным, наблюдатель умножит aн на массу частицы и скажет, что это произведение представляет собой силу Fн, действующую на частицу. Fн = m aн. Выразим aн из (1): aн = aн - 2 vнΩ – mΩ2R (2) Умножим обе части на m и получим: Fн = F – 2mvнΩ – mΩ2R (3), где F=ma и. Т.о видим, что по отношению к вращающейся СО на частицу помимо «истиной» силы F будут действовать 2 добавочные силы: – 2mvнΩ – сила Кориолиса; – mΩ2R – наз-ся центробежной, которая не зависит от скорости vн. Вторая сила инерции(Кориолиса) по своему характеру отличается от всех других сил, которые мы встречали. Эта сила действует только на движ-ся частицы и зависит от направления её движения. В то же время эта сила оказывается независящей от положения частицы в СО. В рассмотренном примере сила F = 2mvнΩ и направлена от оси вращения. Можно показать в общем случае сила Кориолиса, действуя на частицу, движется с произв-й скоростью vн относительно вращающейся с угловой скоростью w СО равна:
и направлено к центру диска. Считая диск неподвижным, наблюдатель умножит aн на массу частицы и скажет, что это произведение представляет собой силу Fн, действующую на частицу. Fн = m aн. Выразим aн из (1): aн = aн - 2 vнΩ – mΩ2R (2) Умножим обе части на m и получим: Fн = F – 2mvнΩ – mΩ2R (3), где F=ma и. Т.о видим, что по отношению к вращающейся СО на частицу помимо «истиной» силы F будут действовать 2 добавочные силы: – 2mvнΩ – сила Кориолиса; – mΩ2R – наз-ся центробежной, которая не зависит от скорости vн. Вторая сила инерции(Кориолиса) по своему характеру отличается от всех других сил, которые мы встречали. Эта сила действует только на движ-ся частицы и зависит от направления её движения. В то же время эта сила оказывается независящей от положения частицы в СО. В рассмотренном примере сила F = 2mvнΩ и направлена от оси вращения. Можно показать в общем случае сила Кориолиса, действуя на частицу, движется с произв-й скоростью vн относительно вращающейся с угловой скоростью w СО равна: 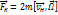 . Эта сила
. Эта сила  оси вращения и скорости частицы, а по величине Fк=2mvнΩsin(
оси вращения и скорости частицы, а по величине Fк=2mvнΩsin(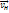 ,
, 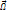 ). При изменении направления скорости меняется и направление силы Кориолиса. Хотя её действие на Земле очень мало, она приводит к некоторым специфическим эффектам. Благодаря этой силе свободно падающее тело должно двигаться не ровно по вертикали, а несколько отклонятся(на восток в северном полушарии и на запад в южном.(как пример берег реки размыт больше, ветра(пассаты)).
). При изменении направления скорости меняется и направление силы Кориолиса. Хотя её действие на Земле очень мало, она приводит к некоторым специфическим эффектам. Благодаря этой силе свободно падающее тело должно двигаться не ровно по вертикали, а несколько отклонятся(на восток в северном полушарии и на запад в южном.(как пример берег реки размыт больше, ветра(пассаты)).
Вопрос 10.РАБОТА И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ. F=-gradU.
Рассмотрим движение мат точки в некот. силовом поле 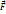 . Если под действием силы
. Если под действием силы 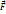 мат. Точка прошла бесконечно малый путь d
мат. Точка прошла бесконечно малый путь d  , то d
, то d  =
= 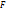 d
d  cos(
cos( ,
, 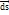 )-работа; dA = F ds cosθ(работа силы F на пути ds); dA =
)-работа; dA = F ds cosθ(работа силы F на пути ds); dA =  *
* 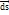 =(
=( ,
, 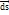 ). Для того чтобы определить работу силы поля на конечном пути, нужно разбить этот путь на беcконечно малые участки ds. dA=
). Для того чтобы определить работу силы поля на конечном пути, нужно разбить этот путь на беcконечно малые участки ds. dA= 
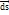 . A=
. A= 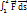 . Из определения работы следует, что сила, направленная
. Из определения работы следует, что сила, направленная  пути, работы не производит. Постоянное силовое поле, не зависящее от t, обладает следующим замечательным свойством: Если в таком поле мат точка движется по замкнутому пути так, что в результате движения точка возвращается в обратное положение, то A = 0. Работа сил поля при переносе частицы из одного положения в др не зависит от вида пути, по которому происходит перенос, а определяется только положениями начальной и конечной точками. При смене направления движения, работа меняет знак(A1c2 + A2d1 = 0). F = mgsinα..A32 = mgh. A312 =U + A12 = mgsinα*l = mgh. Т.к. работа сил поля не зависит от вида переноса, а определяется только крайними точками. Примем для этого какую-либо точку пространства, обозначим через О начало отсчета и будем рассматривать работу, совершаемую силами поля при переходе частицы из этой точки в произвольную точку. Обозначим эту A= - U. Величина U, т.е. взятая с обратным знаком работа при переходе из O в P называется потенциальной энергией частицы P. U=U(x,y,z). Работа сил поля A12 =U1 – U2, где U1 и U2 – значения потенциальной энергии в этих точках. Рассмотрим 2 бесконечно близкие точки P и P’ .
пути, работы не производит. Постоянное силовое поле, не зависящее от t, обладает следующим замечательным свойством: Если в таком поле мат точка движется по замкнутому пути так, что в результате движения точка возвращается в обратное положение, то A = 0. Работа сил поля при переносе частицы из одного положения в др не зависит от вида пути, по которому происходит перенос, а определяется только положениями начальной и конечной точками. При смене направления движения, работа меняет знак(A1c2 + A2d1 = 0). F = mgsinα..A32 = mgh. A312 =U + A12 = mgsinα*l = mgh. Т.к. работа сил поля не зависит от вида переноса, а определяется только крайними точками. Примем для этого какую-либо точку пространства, обозначим через О начало отсчета и будем рассматривать работу, совершаемую силами поля при переходе частицы из этой точки в произвольную точку. Обозначим эту A= - U. Величина U, т.е. взятая с обратным знаком работа при переходе из O в P называется потенциальной энергией частицы P. U=U(x,y,z). Работа сил поля A12 =U1 – U2, где U1 и U2 – значения потенциальной энергии в этих точках. Рассмотрим 2 бесконечно близкие точки P и P’ .
Работа этих сил при P→(переходе)P’ A= - dU, но с другой стороны d 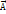 =
=  *d
*d  =
=  *d
*d  dA= FSds. Таким образом: - dU = FSds =>
dA= FSds. Таким образом: - dU = FSds => 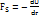 = -
= - 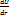 (3) F = - grad U= -
(3) F = - grad U= -  U (
U ( - набла – вектор =
- набла – вектор = 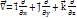 ). F=
). F=