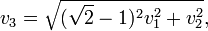С Законом сохр импульса связано важное свойство массы – закон сохр массы. Рассмотрим для замкн сист частиц точку, назыв центром инерции системы. Координаты центра инерции представл собой среднее знач координат частиц. Причем коорд каждой частицы считаются столько раз, сколько единичная масса содерж в массе частицы. Если даны частицы: m1, x1; m2, x2; …;mn, xn; то координаты центра масс: X=(m1x1+…+…mnxn)/(m1+…+mn); Центр инерц обладает свойством: он движется с постоянной скоростью, в то время как отдельные частицы, входящие в замкн сист, могут перемещ со скор, измен со временем.  =d
=d 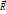 /dt=(m1(d
/dt=(m1(d  1/dt)+…+mi(d
1/dt)+…+mi(d  i/dt))/(m1+…+mi)=(m1
i/dt))/(m1+…+mi)=(m1  1+…+mi
1+…+mi  i)/(m1+…+mi);
i)/(m1+…+mi);  =
= 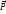 /M;
/M; 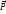 =M
=M  ; M=m1+…+mi=const – закон сохр массы, т.е. масса сложного тела равна сумме масс его частей. Этот з-н является следствием з-на сохр импульса. Т.к. скорость центра инерции замкнут сист частиц не меняется со временем, то связав с центром инерц сист инерц, то получ некую сист отсчета, назыв сист центра масс. Полный импульс в этой сист=0.Это часто упрощ опис движ частиц.
; M=m1+…+mi=const – закон сохр массы, т.е. масса сложного тела равна сумме масс его частей. Этот з-н является следствием з-на сохр импульса. Т.к. скорость центра инерции замкнут сист частиц не меняется со временем, то связав с центром инерц сист инерц, то получ некую сист отсчета, назыв сист центра масс. Полный импульс в этой сист=0.Это часто упрощ опис движ частиц.
Задачу о движении 2 частиц можно свести к задаче о движении 1 частицы с некоторой модифицированной массой, которая называется модифицированной. Рассмотрим движение 2 частиц с массами м1,м2 и скоростями v1,v2 в системе центра инерции обеих частиц. В этой системе m1v1+m2v2=0; Введем относ скор движ част:  =
=  1-
1-  2. m1(
2. m1( +
+  2)+m2
2)+m2  2=0;
2=0;  2=-m1
2=-m1  /(m1+m2);
/(m1+m2);  1=m2
1=m2  /(m1+m2); E=m1v12/2+m2v22/2+u(r),r=r1-r2; E=(m1/2)m22v2/(m1+m2)2+(m2/2)m12v2/
/(m1+m2); E=m1v12/2+m2v22/2+u(r),r=r1-r2; E=(m1/2)m22v2/(m1+m2)2+(m2/2)m12v2/
(m1+m2)2+u(r)=m1m2v2(m1+m2)/2/(m1+m2)2+u(r)=m1m2v2/2/(m1+m2)+u(r)=  v2/2+u(r),
v2/2+u(r),  =m1m2/(m1+m2)-приведенная масса.
=m1m2/(m1+m2)-приведенная масса.
15.Динамика мат точки.3 з-на Ньютона.
мат точка-твердое тело очень малых размеров. Характериз очень мало деформацией. З-н инерции-1 з-н Ньютона: Свободное движение, как и др. движения, выглядит различно в разных системах отсчета. Однако,если в кач-ве СО выбрать СО, связанную с каким-либо свободно движущимся телом, то в такой СО свободно движение др тел выглядит особо просто. Оно происходит равномерно и прямолинейно. Это утверждение состовляет содержание так называемого Закона инерции.СО, связ сщ свободно движ сист, назыв инерц СО.
2ой з-н Ньютона-дифф з-н движения,опис завис ускорения тела от равнодействующей всех прилож к телу сил:
Незамкнутая система:
d 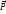 /dt=
/dt= 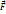 ; d(m
; d(m  )/dt=
)/dt= 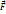 ; m(d
; m(d  /dt)=
/dt)= 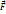 ; m
; m  =
= 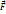 ;
;
3ий з-н Ньютона-мат точки попарно действуют друг на др с силами, имеющими одинаковую природу, направленными вдоль прямой, соед эти точки, равноми по модулю и противоположными по напрвлению. 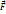 1+
1+ 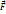 2+…+
2+…+ 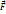 N=0.
N=0.
Замкнутая сист из 2ух тел:
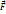 1+
1+ 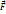 2=0;
2=0; 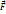 1=-
1=- 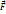 2;
2;
16.З-н всемирного тяготения(ЗВТ). Космические скорости.
ЗВТ:Cила гравитационного притяжения между двумя материальными точками массы m1 и m2, разделенными расстоянием R, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть: F=Gm1m2/R2, здесь G – гравитац постоянная.
Рассмотрим движ 2 тел, притяг друг к др по 3ВТ. Пусть масса одного из из тел будет М много больше массы др тела m. Точечное тело m движется вокруг земли М. Поkt центр сил.
Простейшим движ в таком поле явл движ равном по окруж с центр в центре поля. Ускор направ к центру окр. a=v2/r; mv2/r=GmM/r2; v= 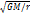 ; v=
; v= 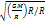 =
= 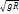 -Первая космич скор. Чтобы тело стало спутником Земли ему необходимо сообщить первую космическую скорость. 2 косм скорость- наименьшая скорость, которую необходимо придать объекту, масса которого пренебрежимо мала по сравнению с массой небесного тела для преодоления гравитационного притяжения этого небесного тела. Mv2/2=GmM/r; v=
-Первая космич скор. Чтобы тело стало спутником Земли ему необходимо сообщить первую космическую скорость. 2 косм скорость- наименьшая скорость, которую необходимо придать объекту, масса которого пренебрежимо мала по сравнению с массой небесного тела для преодоления гравитационного притяжения этого небесного тела. Mv2/2=GmM/r; v= 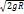 ;
;
Для того чтобы покинуть пределы солнечной системы, тело должно преодолеть, кроме сил притяжения к Земле, также силы притяжения к Солнцу.
Необходимая для этого скорость называется 3 косм. скор.