Периодом колебаний Т называется наименьший промежуток времени, за который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент, выбранный произвольно. При этом фаза получает приращение 2  :
:
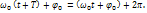 Отсюда получается, что
Отсюда получается, что 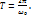 Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой нити длиной L и колеблющейся под действием силы тяжести без трения. Частота малых колебаний зависит от длины маятника
Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой нити длиной L и колеблющейся под действием силы тяжести без трения. Частота малых колебаний зависит от длины маятника 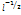 , но не от массы тела. Формула для периода колебаний математического маятника называется формулой Томсона. Согласно период колебаний математического маятника пропорционален его длине в степени 1/2. При небольших углах отклонения
, но не от массы тела. Формула для периода колебаний математического маятника называется формулой Томсона. Согласно период колебаний математического маятника пропорционален его длине в степени 1/2. При небольших углах отклонения 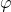 физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F.
физический маятник так же совершает гармонические колебания. Будем считать, что вес физического маятника приложен к его центру тяжести в точке С. Силой, которая возвращает маятник в положение равновесия, в данном случае будет составляющая силы тяжести – сила F. 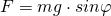 Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла
Знак минус в правой части означает то, что сила F направлена в сторону уменьшения угла α. С учетом малости угла 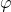 . Так как угол маленький, у нас получается, что F равно:
. Так как угол маленький, у нас получается, что F равно: 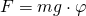 Для вывода закона движения физического маятников используем основное уравнение динамики вращательного движения:
Для вывода закона движения физического маятников используем основное уравнение динамики вращательного движения: 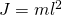 Так как момент силы определить в явном виде нельзя. Надо записать дифференциальное уравнение колебаний физического маятника:
Так как момент силы определить в явном виде нельзя. Надо записать дифференциальное уравнение колебаний физического маятника: 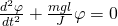 Сравнивая полученное выражение с уравнением гармонических колебаний:
Сравнивая полученное выражение с уравнением гармонических колебаний: 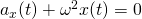 Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:
Из уравнения видно, что циклическая частота пружинного маятника будет иметь вид:  Тогда период колебаний математического маятника будет равен:
Тогда период колебаний математического маятника будет равен:
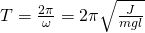
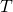 — Период физического маятника.
— Период физического маятника. 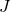 — Момент силы маятника относительно оси вращения.
— Момент силы маятника относительно оси вращения. 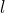 — Расстояние от оси вращения до центра масс.
— Расстояние от оси вращения до центра масс. 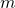 — Масса маятника.
— Масса маятника. 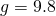 — Ускорение свободного падения
— Ускорение свободного падения
37. Если известен момент инерции тела относительно оси, проходящей через его центр масс, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера: момент инерции тела I относительно произвольной оси равен сумме момента его инерции IС относительно параллельной оси, проходящей через центр масс тела, и произведения массы т тела на квадрат расстояния а между осями: 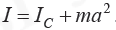
Доказательство:
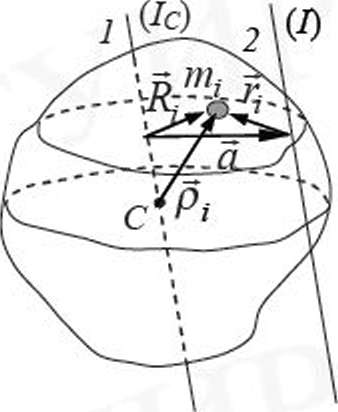 Пусть
Пусть 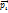 - радиус-вектор i-ro элемента тела относительно центра масс. Радиус-вектор центра масс системы частиц относительно начала отсчета выбранной системы отсчета равен =
- радиус-вектор i-ro элемента тела относительно центра масс. Радиус-вектор центра масс системы частиц относительно начала отсчета выбранной системы отсчета равен = 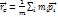 по определению. В системе центра масс
по определению. В системе центра масс 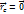 и, следовательно, относительно центра масс суммарный вектор
и, следовательно, относительно центра масс суммарный вектор 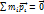 .Но
.Но 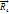 составляющая вектора но
составляющая вектора но 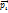 , перпендикулярная осям 1 и 2. Следовательно, если суммарный вектор равен нулю, то сумма его составляющих в плоскости, перпендикулярной осям 1 и 2, также равна нулю.
, перпендикулярная осям 1 и 2. Следовательно, если суммарный вектор равен нулю, то сумма его составляющих в плоскости, перпендикулярной осям 1 и 2, также равна нулю.






