Основные понятия
Определение. Линейной неоднородной системой дифференциальных уравнений (ЛНДС) с постоянными коэффициентами называется система вида:
 (1)
(1)
где  заданные действительные числа,
заданные действительные числа,  заданные непрерывные на промежутке
заданные непрерывные на промежутке  функции, из которых хотя бы одна на
функции, из которых хотя бы одна на  не равна тождественно нулю.
не равна тождественно нулю.
Теорема 1 (структура общего решения ЛНДС).
Общее решение ЛНДС (1) на промежутке  представляет собой сумму общего решения соответствующей ЛОДС и какого-нибудь частного решения ЛНДС (1), т.е.
представляет собой сумму общего решения соответствующей ЛОДС и какого-нибудь частного решения ЛНДС (1), т.е.

Метод вариации произвольных постоянных
1) Рассмотрим этот метод для решения ЛНДС 2-го порядка:
 (2)
(2)
Пусть общее решение соответствующей однородной системы получено в виде:
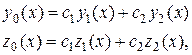
где  произвольные постоянные.
произвольные постоянные.
Будем искать частное решение ЛНДС (2) в виде:
 (3)
(3)
где  функции, которые находятся из решения системы:
функции, которые находятся из решения системы:

Решая систему, определим 
Пусть  и
и  Интегрируя эти выражения, получим
Интегрируя эти выражения, получим 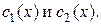 Подставим найденные
Подставим найденные  в формулы (3), получим частное решение ЛНДС (2):
в формулы (3), получим частное решение ЛНДС (2):
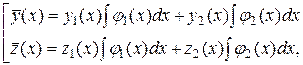
Тогда общее решение ЛНДС (2) запишется в виде:

2) Пусть система (1) записана в матричной форме, причем:

Тогда:
 (4)
(4)
Общее решение ЛНДС (4) можно записать в виде:

где с – матрица-столбец из произвольных постоянных  ,
,  частное решение ЛНДС (4),
частное решение ЛНДС (4),  фундаментальная матрица, ее столбцы линейно-независимые решения ЛОДС.
фундаментальная матрица, ее столбцы линейно-независимые решения ЛОДС.
По методу вариаций произвольных постоянных частное решение ЛНДС (4) запишется в виде:

где  обратная матрица для матрицы
обратная матрица для матрицы 
Теорема 2. Пусть в формуле (4)

где  заданное действительное число,
заданное действительное число,  матрица, составленная из многочленов степени m c постоянными коэффициентами.
матрица, составленная из многочленов степени m c постоянными коэффициентами.
Тогда ЛНДС (4) имеет частное решение вида:
 (5)
(5)
где s равно кратности числа 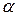 как корня характеристического уравнения матрицы А;
как корня характеристического уравнения матрицы А;  матрица, составленная из многочленов степени m+s с неопределенными коэффициентами, которые определяются путем подстановки функции (5) в (4) вместо Y (x) и приравнивания коэффициентов при подобных членах в правой и левой частях полученного равенства.
матрица, составленная из многочленов степени m+s с неопределенными коэффициентами, которые определяются путем подстановки функции (5) в (4) вместо Y (x) и приравнивания коэффициентов при подобных членах в правой и левой частях полученного равенства.
Теорема 3. Пусть в формуле (4)

где  заданные действительные числа,
заданные действительные числа,  матрицы, составленные из многочленов степени
матрицы, составленные из многочленов степени  соответственно с постоянными коэффициентами. Тогда ЛНДС (4) имеет частное решение вида:
соответственно с постоянными коэффициентами. Тогда ЛНДС (4) имеет частное решение вида:
 (6)
(6)
где  равно кратности числа
равно кратности числа 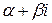 как корня характеристического уравнения матрицы А,
как корня характеристического уравнения матрицы А,  матрицы, составленные из многочленов степени m+s c неопределенными коэффициентами, которые определяются путем подстановки функции (6) в (4) вместо Y (x) и приравнивания коэффициентов при подобных членах в правой и левой частях полученного равенства.
матрицы, составленные из многочленов степени m+s c неопределенными коэффициентами, которые определяются путем подстановки функции (6) в (4) вместо Y (x) и приравнивания коэффициентов при подобных членах в правой и левой частях полученного равенства.
Примеры с решениями
Пример 1. Решить систему:

Решение. Решим эту систему методом вариации произвольных постоянных.
1) Найдем общее решение соответствующей ЛОДС:

Ее характеристическое уравнение имеет вид: 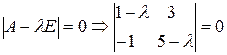

Тогда общее решение ЛОДС составляют функции:

где 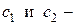 произвольные постоянные,
произвольные постоянные,  постоянные, которые надо выразить через
постоянные, которые надо выразить через  с помощью подстановки
с помощью подстановки 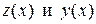 во второе уравнение ЛОДС:
во второе уравнение ЛОДС:

Приравнивая коэффициенты при подобных членах этого равенства, получим выражения для  через
через  :
:

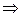

Итак, общее решение ЛОДС имеет вид:

2) Найдем частное решение ЛНДС по методу вариации произвольных постоянных:
 (*)
(*)
Для нахождения функций  составим систему уравнений:
составим систему уравнений:
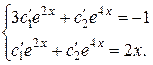

где  любая постоянная, пусть
любая постоянная, пусть 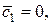 тогда:
тогда:
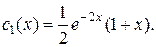

где 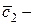 любая постоянная, пусть
любая постоянная, пусть  тогда:
тогда:

Подставим  в (*):
в (*):

Упростим  и
и  :
:
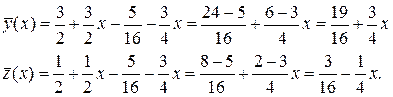
Итак, частное решение ЛНДС составляют функции:

3) Запишем общее решение ЛНДС:
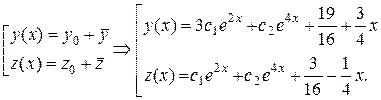

Пример 2. Решить систему:
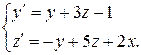
в матричном виде.
Решение.
Обозначения: 
Тогда данная система запишется в матричном виде:

1) Сначала решим однородную систему:
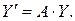
Ее характеристическое уравнение:


Найдем собственные векторы для каждого собственного значения матрицы А.

Пусть  соответствует вектор
соответствует вектор 
Тогда 
Значит:  т.е.
т.е. 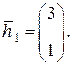

Пусть  соответствует вектор
соответствует вектор 
Тогда 
Значит:  т.е.
т.е. 
Итак, фундаментальная система решений ЛОДС:
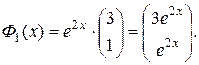

Тогда фундаментальная матрица Ф (x) для ЛОДС имеет вид:

Следовательно, общее решение ЛОДС запишется в виде:

где  и
и  – произвольные постоянные.
– произвольные постоянные.
2) Методом вариации произвольных постоянных найдем частное решение ЛНДС:


Тогда

Вычислим

Значит:

Вычислим интегралы:


В результате получим:

Получили частное решение ЛНДС:

Следовательно, можно записать общее решение ЛНДС:


Пример 3. Решить систему:
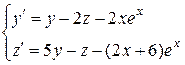
Решение.
1) Решим соответствующую ЛОДС:

Ее характеристическое уравнение имеет вид: 

Пусть общим решением ЛОДС будут функции:

где 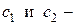 произвольные постоянные,
произвольные постоянные,  постоянные, которые надо выразить через
постоянные, которые надо выразить через  с помощью подстановки
с помощью подстановки  в первое уравнение ЛОДС:
в первое уравнение ЛОДС:

Приравняем коэффициенты при  и
и 
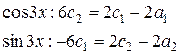
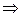

Следовательно, общее решение ЛОДС составляют функции:

2) Найдем частное решение ЛНДС методом неопределенных коэффициентов.

где  матрица-столбец из многочленов первой степени (m =1).
матрица-столбец из многочленов первой степени (m =1).


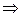

Подставляя  ,
,  ,
,  ,
,  в заданную систему (ЛНДС) и приравнивая в полученных равенствах коэффициенты при подобных слагаемых, получим систему относительно неизвестных
в заданную систему (ЛНДС) и приравнивая в полученных равенствах коэффициенты при подобных слагаемых, получим систему относительно неизвестных 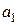 ,
,  ,
,  ,
, 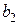 :
:

Разделим оба уравнения на 

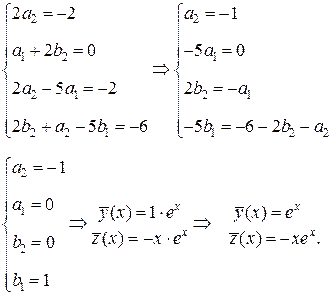
3) Следовательно, общее решение данной ЛНДС составят функции:

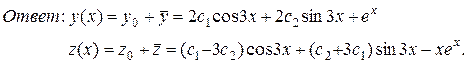
Пример 4. Решить систему:

Решение. В данной системе неизвестных функций три:

1) Найдем общее решение соответствующей однородной системы:

Ее характеристическое уравнение имеет вид:


 кратности 2
кратности 2 

Пусть  фундаментальная система решений ЛОДС.
фундаментальная система решений ЛОДС.

Тогда общее решение ЛОДС можно записать следующим образом:

где  ,
,  ,
,  произвольные постоянные.
произвольные постоянные.
Итак, общее решение ЛОДС составляют три функции:

2) Найдем частное решение ЛНДС методом неопределенных коэффициентов.

Отсюда следует, что частное решение ЛНДС будем подбирать следующим образом:

где  и
и  неизвестные матрицы-столбцы из различных чисел.
неизвестные матрицы-столбцы из различных чисел.
Найдем  и
и 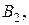 подставляя в ЛНДС.
подставляя в ЛНДС.
Так как  то
то 








Значит, частное решение ЛНДС найдено:

3) Запишем общее решение ЛНДС:


Пример 5. Решить задачу Коши:

Решение.
1) Решим соответствующую ЛОДС:

Ее характеристическое уравнение имеет вид:
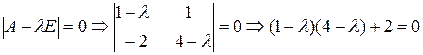

Если  , то
, то 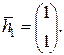
Если  , то
, то 
Тогда 
Общее решение ЛОДС запишется в виде:

Следовательно, общее решение ЛОДС составляют функции:

где  и
и  произвольные постоянные.
произвольные постоянные.
2) Найдем частное решение ЛНДС.
Так как  то
то

Подставим  и
и  в ЛНДС (матричного вида):
в ЛНДС (матричного вида):




(*)  где
где  ,
, 
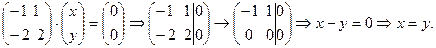
Пусть  тогда
тогда 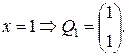
(**) 
Пусть  тогда
тогда 

Значит, 
Частное решение ЛНДС запишется в виде:

3) Следовательно, общее решение ЛНДС задается двумя функциями:
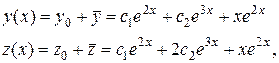
4) Найдем решение задачи Коши. Подставим условия  в общее решение:
в общее решение:

Найденные значения  подставим в общее решение:
подставим в общее решение:
 решение задачи Коши.
решение задачи Коши.

Примеры
Решить ЛНДС методом неопределенных коэффициентов:
1. 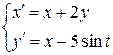
2. 
3. 
4. 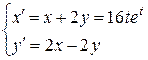
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 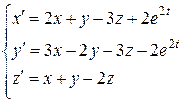
15. 
Решить ЛНДС методом вариации:
16. 
17. 
18. 
Решить задачу Коши:
19. 
20. 
Ответы


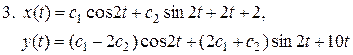



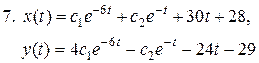



11. 
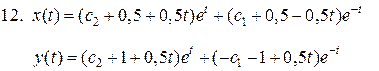








Учебное издание
РУДАКОВСКАЯ Елена Георгиевна
РУШАЙЛО Маргарита Федоровна
РИГЕР Татьяна Викторовна
ХЛЫНОВА Татьяна Вячеславовна
КАЗАНЧЯН Манушак Сережаевна
СИТИН Артем Геннадьевич






