Дифференциальные уравнения второго порядка, допускающие понижение порядка
Основные понятия
Определение 1. Уравнение вида:
 (1)
(1)
называется дифференциальным уравнением второго порядка. Если из этого уравнения выразить

то оно называется разрешенным относительно второй производной.
Определение 2. Общим решением уравнения (1) называется семейство функций, зависящее от двух произвольных постоянных  и
и  :
:

или 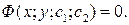
В первом случае его называют общим решением, во втором – общим интегралом уравнения (1).
Определение 3. Задачей Коши для уравнения (1) и заданных начальных условий: 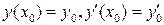 называется поиск частного решения этого уравнения, удовлетворяющего этим начальным условиям:
называется поиск частного решения этого уравнения, удовлетворяющего этим начальным условиям:

где  и
и 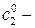 определенные числа, полученные из общего решения при подстановке в него начальных условий.
определенные числа, полученные из общего решения при подстановке в него начальных условий.
Уравнения второго порядка, допускающие понижение порядка
1) Уравнение не содержит явно  и
и 
Пусть дифференциальное уравнение второго порядка имеет вид:
 (2)
(2)
Тогда, учитывая равенство:  получим:
получим:

Следовательно, общее решение уравнения (2) задается функцией:

2) Уравнение не содержит явно 
Пусть уравнение (1) имеет вид:
 (3)
(3)
Для решения такого уравнения выполняется замена:

Эта замена понижает порядок уравнения, приводя уравнение (3) к ДУ первого порядка:

Решим полученное уравнение относительно функции  Получим общее решение этого уравнения:
Получим общее решение этого уравнения:

где  произвольная постоянная.
произвольная постоянная.
Далее, подставив в полученное решение  получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:

Откуда получим:

где 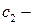 произвольная постоянная.
произвольная постоянная.
Итак, получено общее решение уравнения (3):

3) Уравнение не содержит явно 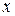
Пусть уравнение (1) имеет вид:
 (4)
(4)
Для решения такого уравнения выполняется замена:

Эта замена понижает порядок уравнения, приводя уравнение (4) к ДУ первого порядка:

Решим полученное уравнение относительно функции  Получим общее решение этого уравнения:
Получим общее решение этого уравнения:

где  произвольная постоянная. Далее, подставив в полученное решение
произвольная постоянная. Далее, подставив в полученное решение  получим дифференциальное уравнение первого порядка:
получим дифференциальное уравнение первого порядка:
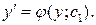
Это уравнение с разделяющимися переменными:

где 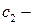 произвольная постоянная.
произвольная постоянная.
Итак, получим общий интеграл уравнения (4):
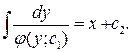
Примеры с решениями
Пример 1. Решить уравнение:

Решение. Это уравнение не содержит  и
и  Учитывая равенство
Учитывая равенство  получим
получим

где  и
и 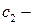 произвольные постоянные.
произвольные постоянные.
Ответ: 
Пример 2. Решить уравнение:
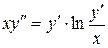
Решение. Это уравнение не содержит явно  . Поэтому выполним замену:
. Поэтому выполним замену:

Такая замена понижает порядок данного уравнения и приводит к уравнению первого порядка:

Это уравнение является однородным первого порядка вида  так как:
так как:

Выполним замену:
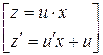
Тогда получим:
 (*)
(*)
Уравнение получилось с разделяющимися переменными. Получим его решение, разделяя переменные, а затем интегрируя:





Получили общее решение уравнения (*). Вернемся к переменным  и
и 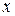 :
:

Подставив  в общее решение, получим дифференциальное уравнение первого порядка:
в общее решение, получим дифференциальное уравнение первого порядка:



где  и
и 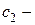 произвольные постоянные.
произвольные постоянные.
Получили общее решение данного уравнения.
Ответ: 
Пример 3. Решить уравнение:
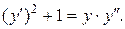
Решение. Это уравнение не содержит явно 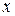 . Поэтому выполним замену:
. Поэтому выполним замену:
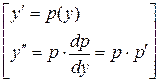
Такая замена понижает порядок данного уравнения и приводит к дифференциальному уравнению первого порядка:
 (**)
(**)
Это уравнение является уравнением с разделяющимися переменными, так как:

Получим его решение, разделяя переменные, а затем интегрируя:

Получили общее решение уравнения (**). Вернемся к переменным 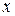 и
и 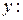

Подставив  в полученное решение, получим дифференциальное уравнение первого порядка c разделяющимися переменными:
в полученное решение, получим дифференциальное уравнение первого порядка c разделяющимися переменными:

где 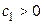 и
и  произвольные постоянные.
произвольные постоянные.
Получили общий интеграл данного уравнения.
Ответ:  .
.
Пример 4. Решить задачу Коши:


Решение. Данное уравнение не содержит явно  Поэтому выполним замену:
Поэтому выполним замену:
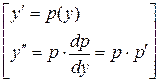
Такая замена приводит к дифференциальному уравнению первого порядка:

 (***)
(***)
Получили уравнение с разделяющимися переменными. Решим его, разделяя переменные, а затем интегрируя:


Получили общее решение уравнения (***). Вернемся к переменным 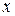 и
и  :
:

Подставив  в полученное решение, получим дифференциальное уравнение первого порядка с разделяющимися переменными:
в полученное решение, получим дифференциальное уравнение первого порядка с разделяющимися переменными:
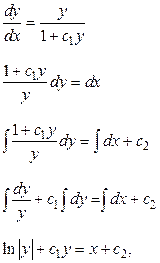
где  и
и  произвольные постоянные.
произвольные постоянные.
Получили общий интеграл данного уравнения. Используем начальные условия: 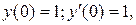 чтобы найти значения
чтобы найти значения  и
и 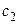 для частного решения данного уравнения.
для частного решения данного уравнения.

Следовательно, решением задачи Коши является частное решение уравнения, получающееся из общего при подстановке в него значений  и
и  :
:

Ответ: 
Примеры
Решить уравнения или задачи Коши:
1. 
2. 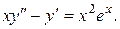
3. 
4. 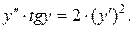
5. 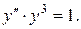
6. 
7. 
8. 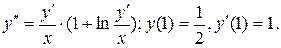
9. 
10. 
11. 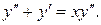
12. 
13. 
14. 
15. 
16. 
17. 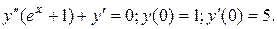
18. 
19. 
20. 
Ответы
1. 
2. 
3. 
4. 
5. 
(или 
6. 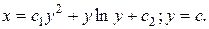
7. 
8. 
9. 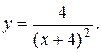
10. 
11. 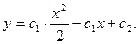
12. 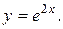
13. 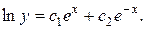
14. 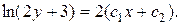
15. 
16. 
17. 
18. 
19. 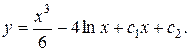
20. 
Замечание. Дифференциальные уравнения вида 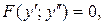 не содержащие в явном виде как независимую переменную
не содержащие в явном виде как независимую переменную  так и искомую функцию
так и искомую функцию  можно решать как уравнение вида 2) или 3).
можно решать как уравнение вида 2) или 3).






