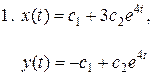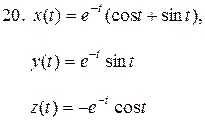1) Найти все собственные значения матрицы A, т.е. числа 
, удовлетворяющие уравнению:
Это уравнение имеет ровно 
корней с учетом их кратности.
2) Найти все линейно независимые собственные и присоединенные к ним векторы матрицы А (их всего должно быть ).
3) Найти функции 
линейно независимые решения системы (5). При этом используют следующие случаи.
а) Случай простого собственного значения
Если 
простое собственное значение матрицы А и 
соответствующий ему собственный вектор А, тогда числу 
в фундаментальной системе решений ЛОДС (5) соответствует функция-столбец:
б) Случай кратного собственного значения
Если кратное собственное значение матрицы А (кратности l) и 
собственный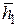 
и присоединенные к нему линейно независимые векторы 
(
, тогда числу в фундаментальной системе решений системы (5) соответствуют функции-столбцы:
(6)
Замечание. Если 
то матрица А имеет собственное значение 
той же кратности 
, что и число . Построенные по формулам (6) функции будут в этом случае комплекснозначными. Выделив в каждой из них действительную и мнимую части, получим набор из 
действительных линейно независимых решений ЛОДС (5), отвечающих паре собственных значений 
в фундаментальной системе решений.
Примеры с решениями
Пример 1. Решить систему:
Решение. Это ЛОДС второго порядка. Решим по методу Эйлера:
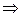
Подставим в заданную систему:
Получим однородную систему линейных уравнений относительно 
и 
. Чтобы эта система имела ненулевое решение, определитель ее должен быть равен нулю:
Это характеристическое уравнение данной системы. Найдем его корни.
Значит, общее решение данной системы можно записать в виде:
где 
и 
произвольные постоянные, а 
и 
выразим через и 
при подстановке 
и 
в первое уравнение системы. Сначала найдем:
Подставим 
в первое уравнение данной системы:
Разделим это равенство на 
Приравнивая коэффициенты при 
и 
, получим выражения для и через и 
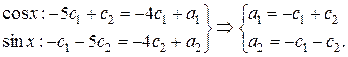
Следовательно, общее решение данной системы запишется в виде:
Пример 2. Решить систему:
Решение. Приведем данную систему к нормальному виду. Для этого сначала исключим 
(*)
Теперь 
из уравнения (*) подставим в первое уравнение данной системы:
(**)
Полученные уравнения (*) и (**) составят систему в нормальном виде:
Решим эту систему методом Эйлера:
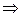
Определитель этой системы должен быть равным нулю:
Получим характеристическое уравнение данной системы. Найдем его корни:
Значит, общее решение данной системы можно записать в виде:
где и произвольные постоянные, а и выразим через и при подстановке и в первое уравнение системы. Для этого найдем
Подставим в первое уравнение данной системы:
Разделим это равенство на 
Приравнивая коэффициенты пр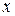и 
и 
, получим выражения и через и 
Следовательно, общее решение данной системы запишется в виде:
Пример 3. Решить задачу Коши:
Решение. Решим систему методом Эйлера:
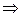
Подставим 
в данную систему:
Определитель полученной системы должен быть равен нулю:
Получим характеристическое уравнение данной системы. Найдем его корни.
Значит, общее решение данной системы можно записать в виде:
где и произвольные постоянные, а и выразим через и при подстановке и в первое уравнение системы.
Для этого найдем 
Подставляем в первое уравнение данной системы:
Приравнивая коэффициенты при 
и 
, получим выражения и через и
Следовательно, общее решение данной системы запишется в виде:
Найдем решение задачи Коши при начальных условиях:
Подставим в общее решение 
Значит, частным решением системы, удовлетворяющим начальным условиям, являются функции:
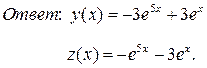
Пример 4. Решить систему:
Решение. Эта система третьего порядка относительно неизвестных функций 
Решим ее матричным способом.
Обозначим матрицы-столбцы:
и 
и матрицу из коэффициентов системы:
Тогда данную систему можно записать в матричном виде:
1) Найдем собственные значения матрицы А из характеристического уравнения:
, т.е. 
2) Найдем собственные векторы А, соответствующие 
Получим ступенчатый вид Гаусса матрицы А.
Решим систему 
Пусть 
тогда 
Значит, собственный вектор 
3) Найдем присоединенные векторы 
и 
к вектору 
Получим ступенчатый вид Гаусса.
Пусть 
тогда 
Пусть 
Итак, 
первый присоединенный вектор к 
Найдем еще один присоединенный к 
вектор 
:
Получим ступенчатый вид Гаусса.
Пусть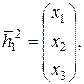 
тогда 
Пусть 
Итак, 
второй присоединенный вектор к
Векторы 
линейно независимые.
4) Построим фундаментальную систему решений данной ЛОДС.
Следовательно, общее решение ЛОДС:
где 
произвольные постоянные.
Пример 5. Решить систему:
Решение. Эта система третьего порядка относительно неизвестных функций Решим ее матричным способом.
Обозначим матрицы-столбцы:
, и матрицу из коэффициентов системы:
Тогда данную систему можно записать в матричном виде:
1) Найдем собственные значения матрицы А из характеристического уравнения:
Получим 
кратности 2 и 
2) Найдем собственные векторы А, соответствующие 
Получим ступенчатый вид матрицы А.
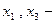свободные неизвестные, 
базисная неизвестная.
Пусть 
тогда 
Итак, 
Пусть 
тогда 
Итак, 
Получим 
и 
два линейно независимых собственных вектора, соответствующие значению 
3) Найдем собственный вектор матрицы А, соответствующий 
Получим ступенчатый вид Гаусса.
Пусть 
Тогда 
свободная неизвестная,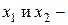 
базисные неизвестные.
Пусть 
, тогда 
Итак, 
третий собственный вектор, соответствующий
Полученные векторы 
линейно независимые.
4) Построим фундаментальную систему решений данной ЛОДС.
Следовательно, общее решение ЛОДС:
= 
где произвольные постоянные.
Примеры
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
Решить задачу Коши:
16. 
17. 
18. 
19. 
20. 
Ответы
