Обыкновенные дифференциальные
Уравнения и системы
(примеры и задачи)
Утверждено Редакционным советом
университета в качестве учебного пособия
Москва
УДК 517.91 (075)
ББК 22.161.6
О-30
Авторы: Е. Г. Рудаковская, М. Ф. Рушайло, Т. В. Ригер, Т. В. Хлынова,
М. С. Казанчян, А. Г. Ситин
Рецензенты:
Доктор физико-математических наук, профессор Российского химико-технологического университета им. Д. И. Менделеева
В. М. Аристов
Доктор технических наук, профессор Российского химико-технологического университета им. Д. И. Менделеева
Л. С. Гордеев
Обыкновенные дифференциальные уравнения и системы (примеры и
О-30 задачи): учеб. пособие / Е. Г. Рудаковская, М. Ф. Рушайло, Т. В.
Ригер, Т. В. Хлынова, М. С. Казанчян, А. Г. Ситин; под ред. Е. Г.
Рудаковской, М. Ф. Рушайло. – М.: РХТУ им. Д. И. Менделеева, 2013. –
116 с.
ISBN 978-5-7237-1118-1
Предложен цикл практических занятий по темам: дифференциальные уравнения первого, второго и n -го порядков, системы линейных дифференциальных уравнений. В каждой теме кратко приведен теоретический материал, разобраны примеры с решениями и предложены примеры для самостоятельного решения с ответами. Пособие может быть использовано на семинарских занятиях, а также для самостоятельной работы, при подготовке к контрольным работам, зачетам и экзаменам.
Предназначается для студентов всех специальностей, обучающихся в РХТУ имени Д. И. Менделеева, так как данный курс является необходимым элементом математического образования студентов технических специальностей, имеющим большое прикладное значение.
УДК 517.91 (075)
ББК 22.161.6
ISBN 978-5-7237-1118-1 © Российский химико-технологический
университет им. Д. И. Менделеева, 2013
Оглавление
Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА.. 4
§1. Дифференциальные уравнения с разделяющимися переменными. 4
§2. Однородные дифференциальные уравнения первого порядка. 10
§3. Линейные дифференциальные уравнения первого порядка. Уравнения Бернулли 17
§4. Дифференциальные уравнения в полных дифференциалах. Уравнения с интегрирующим множителем. 24
Глава 2. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ВТОРОГО ПОРЯДКА.. 34
§1. Дифференциальные уравнения второго порядка, допускающие понижение порядка 34
§2. Линейные дифференциальные уравнения второго порядка. 42
§3. Решение линейных неоднородных дифференциальных уравнений второго порядка с постоянными коэффициентами. 47
§4. Линейные дифференциальные уравнения n- го порядка с постоянными коэффициентами. 63
Глава 3. ЛИНЕЙНЫЕ ДИФФЕРЕНЦИАЛЬНЫЕ СИСТЕМЫ n -го ПОРЯДКА С ПОСТОЯННЫМИ КОЭФФИЦИЕНТАМИ.. 72
§1. Линейные дифференциальные системы n -го порядка с постоянными коэффициентами. Метод исключения. 72
§2. Линейные однородные системы дифференциальных уравнений с постоянными коэффициентами. 79
§3. Линейные неоднородные системы дифференциальных уравнений с постоянными коэффициентами. 97
Глава 1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА
Дифференциальные уравнения с разделяющимися переменными
Основные понятия
Определение 1. Уравнение, связывающее неизвестную функцию  , ее аргумент
, ее аргумент 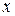 и производную
и производную  или их дифференциалы dx и dy, называется дифференциальным уравнением первого порядка, т.е.
или их дифференциалы dx и dy, называется дифференциальным уравнением первого порядка, т.е.
 (1)
(1)
Если из этого уравнения можно выразить y´(x), то уравнение примет вид:

при этом его называют уравнением, разрешенным относительно производной.
Определение 2. Решением дифференциального уравнения (1) называется любая дифференцируемая функция  , которая при ее подстановке в уравнение (1) обращает его в верное равенство. При этом, если она задана явно, то используют термин решение, а если неявно, то говорят интеграл. График решения называется интегральной кривой. Процесс нахождения решений дифференциального уравнения называется интегрированием этого уравнения.
, которая при ее подстановке в уравнение (1) обращает его в верное равенство. При этом, если она задана явно, то используют термин решение, а если неявно, то говорят интеграл. График решения называется интегральной кривой. Процесс нахождения решений дифференциального уравнения называется интегрированием этого уравнения.
Определение 3. Общим решением (или общим интегралом) дифференциального уравнения называется множество всех без исключения решений этого уравнения. Множество таких решений образуется с помощью произвольной постоянной с:
 – в явном виде – общее решение
– в явном виде – общее решение
и  – в неявном виде – общий интеграл уравнения.
– в неявном виде – общий интеграл уравнения.
Определение 4. Частным решением, или частным интегралом дифференциального уравнения (1) называется функция  или
или  , полученная из общего решения или общего интеграла при определенном значении произвольной постоянной
, полученная из общего решения или общего интеграла при определенном значении произвольной постоянной  .
.
Определение 5. Поиск частного решения дифференциального уравнения, удовлетворяющего дополнительному начальному условию:
 ,
,
где  и
и 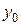 – заданные числа, называется задачей Коши.
– заданные числа, называется задачей Коши.
Дифференциальные уравнения с разделяющимися переменными
Определение 6. Дифференциальным уравнением с разделяющимися переменными называется уравнение вида:
 (2)
(2)
или уравнение вида:
 (3)
(3)
Чтобы уравнения (2) и (3) можно было проинтегрировать, необходимо привести их к уравнениям с разделёнными переменными, т.е. при дифференциалах dx и dy должны быть множители, зависящие соответственно от x и от y.
Решим уравнение (2) в общем виде:

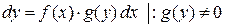
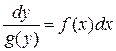

Пусть  , а
, а  , тогда выражение
, тогда выражение
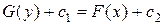 или
или  , где
, где  является интегралом уравнения (2). Остается проверить, что не потеряны решения при делении уравнения на выражения, зависящие от переменных. Решим уравнение
является интегралом уравнения (2). Остается проверить, что не потеряны решения при делении уравнения на выражения, зависящие от переменных. Решим уравнение  . Если оно имеет решение, являющееся и решением уравнения (2), то оно тоже будет присоединено к общему интегралу этого уравнения.
. Если оно имеет решение, являющееся и решением уравнения (2), то оно тоже будет присоединено к общему интегралу этого уравнения.
Решим уравнение (3) в общем виде:




 уравнение с разделенными переменными
уравнение с разделенными переменными


 общий интеграл уравнения (3)
общий интеграл уравнения (3)
К полученному интегралу могут быть добавлены решения уравнений:  и
и  , если они являются для заданного уравнения решениями.
, если они являются для заданного уравнения решениями.
Некоторые дифференциальные уравнения можно привести к уравнениям с разделяющимися переменными. Например, уравнения вида:
 или
или 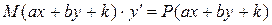 ,
,
где  и
и  – некоторые числа, приводят к виду (2) или (3) с помощью замены:
– некоторые числа, приводят к виду (2) или (3) с помощью замены:

Примеры с решениями
Пример 1. Решить уравнение: 
Решение. Данное уравнение является уравнением с разделяющимися переменными вида (2), так как его можно переписать в виде:

Приведем его к уравнению с разделенными переменными:



Теперь его можно интегрировать:


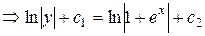 , обозначим
, обозначим 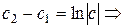

Получим общее решение уравнения.
Проверим, не потеряно ли решение  ?
?
Подставим в заданное уравнение  , а тогда и
, а тогда и  . Получим
. Получим  .
.
Значит, 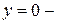 решение данного уравнения, но оно принадлежит полученному общему решению при
решение данного уравнения, но оно принадлежит полученному общему решению при  .
.
Ответ:  .
.
Пример 2. Решить уравнение:

Решение. Соберём слагаемые, содержащие  и
и  :
:


Это уравнение вида (3), так как:




Разделим переменные:

Интегрируя, получаем:


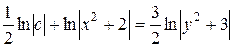 , где
, где 

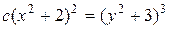
 это общий интеграл уравнения.
это общий интеграл уравнения.
Так как уравнения  и
и  не имеют действительных решений, то при интегрировании уравнения не могли быть потеряны решения.
не имеют действительных решений, то при интегрировании уравнения не могли быть потеряны решения.
Ответ: 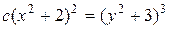 .
.
Пример 3. Решить задачу Коши:


Решение. Уравнение  является уравнением с разделяющимися переменными вида (3), так как:
является уравнением с разделяющимися переменными вида (3), так как:


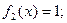

Разделим переменные, поделив уравнение на 

Интегрируя, получим:


 .
.
Обозначим  :
:


 общий интеграл уравнения.
общий интеграл уравнения.
Используя начальное условие: 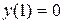 , получим частное решение
, получим частное решение
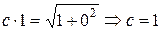 .
.
Значит, частное решение данного уравнения при заданном начальном условии имеет вид:
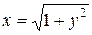
Ответ: 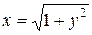 .
.
Пример 4. Решить уравнение:
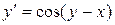 .
.
Решение. Выполним замену:  .
.
Тогда уравнение изменится:
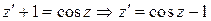 .
.
Получилось уравнение с разделяющимися переменными вида (2), так как

 . Разделим переменные:
. Разделим переменные:
 .
.
Интегрируя, получим:
 .
.
Обозначим  , тогда
, тогда  .
.
Так как 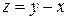 , то общим интегралом будет:
, то общим интегралом будет:  .
.
Решим уравнение  . Тогда z
. Тогда z  =0.
=0.
Подставим в заданное уравнение и получим тождество: 0+1=1. Значит,  или
или  – решение для данного уравнения, но не входит в общий интеграл.
– решение для данного уравнения, но не входит в общий интеграл.
Ответ:  .
.
Примеры
Решить уравнения или задачи Коши:
1. 
2. 
3. 
4. 
5. 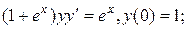
6. 
7. 
8. 
9. 
10. 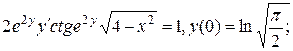
11. 
12. 
13. 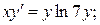
14. 
15. 
16. 
17. 
18. 
19. 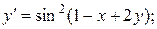
20. 
Ответы
1. 
2. 
3. 
4. 
5. 
6. 
7. 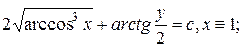
8. 
9. 
10. 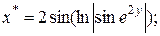
11. 
12. 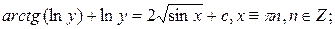
13. 
14. 
15. 
16. 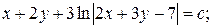
17. 
18. 
19. 
20. 






