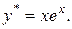Определения и методы решения

Определение 1. Уравнение вида:
 (1)
(1)
где  и
и  – заданные непрерывные функции на
– заданные непрерывные функции на 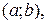 называется линейным дифференциальным уравнением (ЛДУ). Если
называется линейным дифференциальным уравнением (ЛДУ). Если 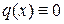 при
при  то уравнение имеет вид:
то уравнение имеет вид:
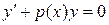
и называется линейным однородным дифференциальным уравнением (ЛОДУ). А если  при
при  то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
то уравнение (1) называется линейным неоднородным дифференциальным уравнением (ЛНДУ).
Метод решения ЛНДУ
1) Метод вариации произвольной постоянной:
· сначала решить соответствующее ЛОДУ, которое является уравнением с разделяющимися переменными:
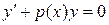




 (2)
(2)
· заменить в формуле (2) постоянную  на неизвестную функцию
на неизвестную функцию  и подставить это выражение вместо
и подставить это выражение вместо  в уравнение (1), предварительно найдя
в уравнение (1), предварительно найдя 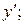
· из полученного уравнения найти функцию 
· записать ответ:

где  произвольная постоянная.
произвольная постоянная.
2) Метод Бернулли:
· выполнить в уравнении (1) замену Бернулли:


 (3)
(3)
· приравнять к нулю выражение

и найти отсюда любое частное решение 




· подставить полученную функцию  в уравнение (3) и найти общее решение
в уравнение (3) и найти общее решение  из этого уравнения;
из этого уравнения;
· записать ответ: 
где  произвольная постоянная.
произвольная постоянная.
Уравнение Бернулли
Определение 2. Уравнение вида
 где
где  и
и  (4)
(4)
называется уравнением Бернулли с показателем 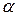 .
.
Уравнение (4) приводится к ЛНДУ(1) с помощью замены:

После этой замены уравнение (1) приводится к следующему:

Это уравнение ЛНДУ относительно функции  Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции
Его можно решать также с помощью замены Бернулли. Но можно и уравнение (4), не проводя замену к функции  , решать методом замены Бернулли непосредственно. При этом функция
, решать методом замены Бернулли непосредственно. При этом функция  будет частным решением уравнения
будет частным решением уравнения

а функция  будет находиться из уравнения
будет находиться из уравнения
 .
.
Замечание 1. При таком решении при  решение
решение  будет всегда потеряно.
будет всегда потеряно.
Замечание 2. Некоторые дифференциальные уравнения первого порядка становятся линейными или уравнениями Бернулли, если в них поменять ролями искомую функцию  и независимую переменную
и независимую переменную 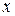 .
.
Примеры с решениями
Пример 1. Решить уравнение:
 .
.
Решение. Уравнение имеет вид (1), где 
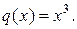 Решим его двумя способами.
Решим его двумя способами.
Способ 1 (метод вариации постоянной)
1) Решим сначала ЛОДУ, соответствующее данному ЛНДУ:

Это уравнение с разделяющимися переменными:



 , где
, где  произвольная постоянная.
произвольная постоянная.
2) Решение данного уравнения ищем в таком же виде, но считаем переменной  т.е.
т.е.

Найдем  и подставим функцию
и подставим функцию  в заданное уравнение:
в заданное уравнение:

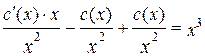


где  произвольная постоянная. Следовательно, общим решением заданного дифференциального уравнения будет:
произвольная постоянная. Следовательно, общим решением заданного дифференциального уравнения будет:

Способ 2 (метод Бернулли)
Выполним в заданном уравнении замену Бернулли:


 . (*)
. (*)
1) Найдем функцию  из уравнения:
из уравнения:


где  любое число.
любое число.
Но так как нас интересует частное решение  , то выберем значение
, то выберем значение  :
:

2) Найдем функцию 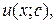 решая уравнение (*) при
решая уравнение (*) при 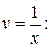

где  – произвольная постоянная.
– произвольная постоянная.
Следовательно, общее решение заданного уравнения можно записать:

Ответ:  .
.
Пример 2. Решить задачу Коши:

Решение. Заданное уравнение является линейным неоднородным дифференциальным уравнением. Решим его методом Бернулли. Для этого сделаем замену:
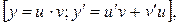
которая приведет к следующему уравнению:

 (**)
(**)
1) Функцию  найдем из уравнения:
найдем из уравнения:

 ,
,
где  любое число,
любое число,


поэтому возьмем  , т.е.
, т.е.
 .
.
2) Найдем функцию  из уравнения (**) при
из уравнения (**) при 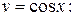
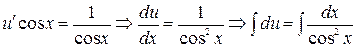

где  – произвольная постоянная.
– произвольная постоянная.
Общее решение данного уравнения:

В полученном общем решении найдем  так, чтобы удовлетворялось условие:
так, чтобы удовлетворялось условие: 

Значит, решением задачи Коши является функция

Ответ:  .
.
Пример 3. Решить уравнение:

Решение. Данное уравнение не является линейным относительно функции  Но если учесть, что
Но если учесть, что

то уравнение можно переписать в виде:

 (5)
(5)
которое является линейным уравнением относительно функции  Решим полученное уравнение методом вариации постоянной:
Решим полученное уравнение методом вариации постоянной:
1) Сначала решаем ЛОДУ:


2) Пусть  тогда
тогда 
Подставим эту функцию в уравнение (5):


где  – произвольная постоянная.
– произвольная постоянная.
Следовательно, общее решение уравнения (5) имеет вид:

Чтобы найти общее решение заданного уравнения, заметим, что при переходе от данного уравнения к уравнению (5) могло быть потеряно решение  . Действительно, подстановкой в исходное уравнение убеждаемся, что
. Действительно, подстановкой в исходное уравнение убеждаемся, что  – решение данного уравнения и оно не попадает в общее решение уравнения (5) ни при каком значении
– решение данного уравнения и оно не попадает в общее решение уравнения (5) ни при каком значении  Поэтому записываем его в ответ.
Поэтому записываем его в ответ.
Ответ: 
Пример 4. Решить уравнение:

Решение. Данное уравнение является уравнением Бернулли с показателем  Решим его методом Бернулли. Для этого выполним замену:
Решим его методом Бернулли. Для этого выполним замену:

 (***)
(***)
1) Функцию  найдем из уравнения:
найдем из уравнения:

где  – любое число (пусть
– любое число (пусть  ), тогда
), тогда

2) Найдем функцию  из уравнения (***) при
из уравнения (***) при  :
:

где  – произвольная постоянная.
– произвольная постоянная.
После преобразований получим:

Следовательно, общее решение данного уравнения запишется следующим образом:

Так как  то в ответ запишем и потерянное решение
то в ответ запишем и потерянное решение 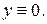
Ответ: 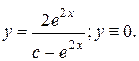
Примеры
Решить ДУ или задачи Коши:
1. 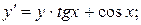
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 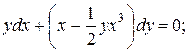
12. 
13. 
14. 
15. 
16. 
17. 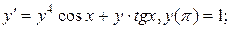
18. 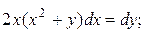
19. 
20. 
Ответы
1. 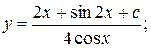
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 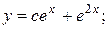
11. 
12. 
13. 
14. 
15. 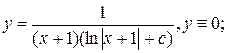
16. 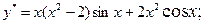
17. 
18. 
19. 
20.