Интегрирующий множитель  удовлетворяет дифференциальному уравнению:
удовлетворяет дифференциальному уравнению:

Однако нет общего метода интегрирования такого уравнения. Рассмотрим частные случаи существования интегрирующих множителей вида:  и
и 
Теорема 1. Пусть в некоторой области D выполнены условия:
1)  непрерывны;
непрерывны;
2) 
3)  является функцией, зависящей только от переменной
является функцией, зависящей только от переменной 
Тогда дифференциальное уравнение (1) имеет интегрирующий множитель, зависящий только от 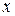 и вычисляемый по формуле:
и вычисляемый по формуле:

Теорема 2. Пусть в некоторой области D выполнены условия:
1)  непрерывны;
непрерывны;
2) 
3)  является функцией, зависящей только от переменной
является функцией, зависящей только от переменной 
Тогда дифференциальное уравнение (1) имеет интегрирующий множитель, зависящий только от  и вычисляемый по формуле:
и вычисляемый по формуле:

Примеры с решениями
Пример 1. Решить уравнение:

Решение. В данном примере
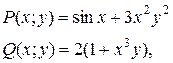
откуда получим:

Значит, данное уравнение в полных дифференциалах. Поэтому существует функция  для которой выполняется равенство:
для которой выполняется равенство:

Составим и решим систему уравнений:

Проинтегрируем по 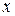 первое уравнение, считая
первое уравнение, считая  постоянным:
постоянным:

 (*)
(*)
Определим функцию  используя второе уравнение системы:
используя второе уравнение системы:
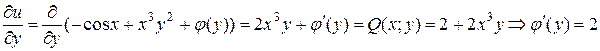

где  произвольная постоянная.
произвольная постоянная.
Подставим  в равенство (*):
в равенство (*):

Таким образом, общим интегралом данного уравнения будет:


Ответ: 
Пример 2. Решить задачу Коши:

Решение. Проверим выполнение условия


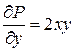 и
и 
 .
.
Следовательно, заданное уравнение в полных дифференциалах. Составим систему уравнений относительно неизвестной функции  для которой выполняется равенство:
для которой выполняется равенство:

Тогда: 
 (**)
(**)
Найдем функцию  используя второе уравнение системы:
используя второе уравнение системы:
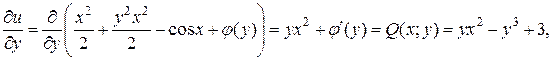


где  произвольная постоянная.
произвольная постоянная.

Подставим найденную  в (**):
в (**):

Таким образом, общий интеграл данного уравнения можно записать:



Найдем число  так, чтобы выполнялось условие:
так, чтобы выполнялось условие: 
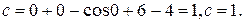
Следовательно, решение задачи Коши находится из общего решения при 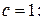

Ответ: 
Пример 3. Решить уравнение:
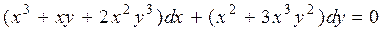
Решение. Проверим условие 

Следовательно, это уравнение не является уравнением в полных дифференциалах. Проверим выполнение условий теоремы 1 существования интегрирующего множителя 

Таким образом, интегрирующий множитель вида 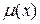 существует и находится по формуле:
существует и находится по формуле:


Умножим заданное уравнение на найденную функцию и получим уравнение в полных дифференциалах:


Поэтому существует  для которой
для которой

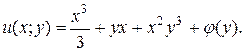 (***)
(***)


где  произвольная постоянная.
произвольная постоянная.
Подставим  в равенство (***):
в равенство (***):

Тогда общий интеграл запишется в виде:

При переходе от заданного уравнения к уравнению в полных дифференциалах было потеряно решение 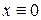 (при делении на
(при делении на 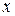 ). Но оно входит в полученное семейство при
). Но оно входит в полученное семейство при 
Ответ: 
Пример 4. Решить уравнение:

Решение. Проверим условие 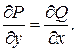

Следовательно, это уравнение не является уравнением в полных дифференциалах. Проверим выполнение условий теоремы 2 существования интегрирующего множителя 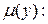

Таким образом, интегрирующий множитель вида  существует и находится по формуле:
существует и находится по формуле:


Умножим заданное уравнение на  и решим полученное уравнение в полных дифференциалах:
и решим полученное уравнение в полных дифференциалах:


Поэтому существует  для которой выполняется равенство:
для которой выполняется равенство:

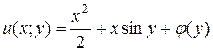 (****)
(****)


где  произвольная постоянная.
произвольная постоянная.
Подставим найденную функцию  в выражение (****):
в выражение (****):

Тогда общий интеграл запишется в виде:

Следовательно, это общий интеграл заданного уравнения.
Ответ: 
Примеры
Решить ДУ или задачи Коши:
1. 
2. 
3. 
4. 
5. 
6. 
7. 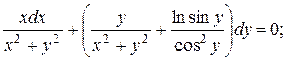
8. 
9. 
10. 
11. 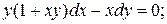
12. 
13. 
14. 
15. 
16. 
17. 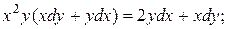
18. 
19. 
Ответы
1. 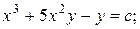
2. 
3. 
4. 
5. 
6. 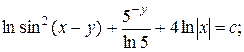
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 




