Основные понятия
Определение 1. Уравнение, вида:
 (1)
(1)
где 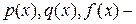 непрерывные на промежутке
непрерывные на промежутке  функции, называется линейным дифференциальным уравнением (ЛДУ) второго порядка. Если
функции, называется линейным дифференциальным уравнением (ЛДУ) второго порядка. Если 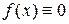 для всех
для всех 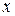 из промежутка
из промежутка  , то уравнение (1) называют линейным однородным дифференциальным уравнением (ЛОДУ):
, то уравнение (1) называют линейным однородным дифференциальным уравнением (ЛОДУ):
 (2)
(2)
Если  то уравнение (1) называют линейным неоднородным дифференциальным уравнением (ЛНДУ).
то уравнение (1) называют линейным неоднородным дифференциальным уравнением (ЛНДУ).
Определение 2. Две функции 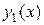 и
и  называются линейно зависимыми на промежутке
называются линейно зависимыми на промежутке  , если для всех
, если для всех  их отношение равно постоянной величине, т.е.
их отношение равно постоянной величине, т.е.  В противном случае, если
В противном случае, если 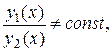 функции называются линейно независимыми на промежутке
функции называются линейно независимыми на промежутке  .
.
Определение 3. Если 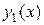 и
и  линейно независимые решения ЛОДУ, то они образуют фундаментальную систему решений этого уравнения.
линейно независимые решения ЛОДУ, то они образуют фундаментальную систему решений этого уравнения.
Теорема 1. Если 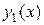 и
и  линейно независимые решения ЛОДУ (2) на промежутке
линейно независимые решения ЛОДУ (2) на промежутке  , то их линейная комбинация
, то их линейная комбинация

где  и
и  произвольные постоянные, является общим решением этого уравнения.
произвольные постоянные, является общим решением этого уравнения.
Теорема 2. Общее решение ЛНДУ второго порядка (1) представляется в виде суммы общего решения 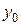 соответствующего ЛОДУ (2) и любого частного решения
соответствующего ЛОДУ (2) и любого частного решения  ЛНДУ (1), т.е.
ЛНДУ (1), т.е.  общее решение ЛНДУ (1).
общее решение ЛНДУ (1).
Теорема 3. Если  частное решение ЛНДУ:
частное решение ЛНДУ:
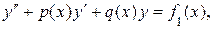
а  частное решение ЛНДУ:
частное решение ЛНДУ:
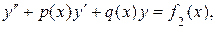
то  является частным решением ЛНДУ:
является частным решением ЛНДУ:

Линейные однородные дифференциальные уравнения с постоянными коэффициентами
Определение 1. Уравнение вида
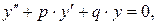 (3)
(3)
где 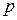 и
и  действительные числа, называется линейным однородным дифференциальным уравнением (ЛОДУ) второго порядка с постоянными коэффициентами.
действительные числа, называется линейным однородным дифференциальным уравнением (ЛОДУ) второго порядка с постоянными коэффициентами.
Метод Эйлера для решения ЛОДУ с постоянными коэффициентами
Частные решения такого уравнения получают с помощью замены:
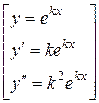 (*)
(*)
Подставляя в уравнение (3) выражения (*), получим:

 (4)
(4)
Уравнение (4) называется характеристическим для данного уравнения (3). Оно является квадратным уравнением, поэтому в зависимости от величины дискриминанта  возможны три случая.
возможны три случая.
1)  Тогда корни характеристического уравнения (4) действительные и различные –
Тогда корни характеристического уравнения (4) действительные и различные –  Они дадут два линейно независимых решения:
Они дадут два линейно независимых решения:  и
и  . Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
. Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:

2)  В этом случае
В этом случае  Поэтому одно решение уравнения (3) будет
Поэтому одно решение уравнения (3) будет  . В качестве второго, линейно независимого с первым, можно взять функцию
. В качестве второго, линейно независимого с первым, можно взять функцию 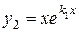 . Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
. Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
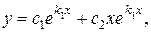
или 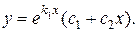
3)  В этом случае корни уравнения (4) комплексно-сопряженные:
В этом случае корни уравнения (4) комплексно-сопряженные:  Тогда в качестве линейно независимых решений можно взять функции
Тогда в качестве линейно независимых решений можно взять функции  и
и  Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:
Следовательно, в этом случае по теореме 1 общее решение уравнения (3) можно записать в виде:

или 
Примеры с решениями
Пример 1. Найти фундаментальную систему решений и общее решение:

Решение. Подставляя  в заданное уравнение, получим характеристическое уравнение:
в заданное уравнение, получим характеристическое уравнение:

Так как корни действительные и различные, то фундаментальную систему решений этого уравнения составят функции:

Тогда общее решение данного уравнения можно записать в виде линейной комбинации:

Ответ: 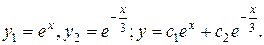
Пример 2. Решить уравнение:
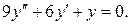
Решение. Характеристическое уравнение:
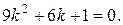

Корни этого уравнения будут действительными и равными:

Тогда фундаментальную систему решений этого уравнения составят функции:

Общее решение запишется как линейная комбинация этих решений:

Ответ: 
Пример 3. Решить уравнение:

Решение. Характеристическое уравнение:

Решим его: 
Корни этого уравнения будут комплексно-сопряженными:

Фундаментальную систему решений этого уравнения составят функции:
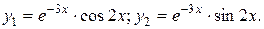
Общее решение запишется как линейная комбинация этих функций:

Ответ: 
Пример 4. Решить задачу Коши:

Решение. Характеристическое уравнение:


Корни этого уравнения действительные и равные:

Фундаментальную систему решений этого уравнения составят функции:

Общее решение запишется как линейная комбинация этих функций:

Найдем частное решение, удовлетворяющее начальным условиям  и
и  Сначала найдем:
Сначала найдем:

Составим систему из двух уравнений, подставляя в общее решение 

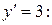

Подставим найденные значения  и
и  в общее решение:
в общее решение:
 это и будет решение задачи Коши.
это и будет решение задачи Коши.
Ответ: 
Примеры
Найти фундаментальную систему решений:
1. 
2. 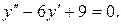
3. 
4. 
5. 
6. 
Найти общее решение уравнения:
7. 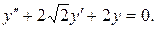
8. 
9. 
10. 
11. 
12. 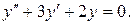
13. 
14. 
15. 
16. 
17. 
18. 
19. 
20. 
Решить задачи Коши или краевые задачи:
21. 
22. 
23. 
24. 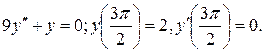
25. 
Ответы
1. 
2. 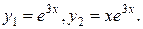
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 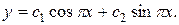
15. 
16. 
17. 
18. 
19. 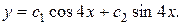
20. 
21. 
22. 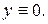
23. 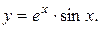
24. 
25. 






