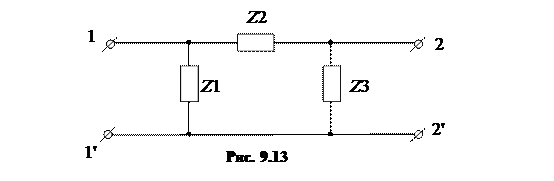
Рассмотрим П-схему четырехполюсника (рис. 9.13).
Определим эквивалентные сопротивления этой схемы при холостом ходе и коротком замыкании.
1. Холостой ход при прямом включении
.
2. Короткое замыкание при прямом включении
.
3. Холостой ход при обратном включении
.
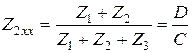4. Короткое замыкание при обратном включении
.
 |
Используя условие обратимости и решая три из этих уравнений относительно коэффициентов A; B; C; D,получим:
; 
; 
; 
.
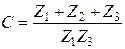Выразив сопротивления через параметры четырехполюсника, получим:
; 
; 
.
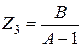Передаточная функция четырехполюсника
Передаточной функцией (коэффициентом передачи) четырехполюсника называется отношение комплексных амплитуд тока или напряжения на выходе и входе четырехполюсника. Различают передаточные функции по току и напряжению
; 
.
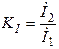Применительно к усилительным устройствам эти коэффициенты носят название коэффициентов усиления по напряжению и по току.
В радиотехнике и технике связи используют также передаточное сопротивление
и передаточную проводимость
.
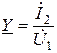Для четырехполюсника, нагруженного произвольным сопротивлением 
, передаточная функция может быть выражена через любую систему коэффициентов четырехполюсника и данное сопротивление нагрузки.
Выразим их через коэффициенты 
формы:
;
.
Модули этих комплексных отношений представляют собой амплитудно-частотные характеристики, а аргументы – фазо-частотные характеристики.
При холостом ходе и коротком замыкании при прямом включении эти коэффициенты примут вид:
При обратном включении, соответственно
Сложные четырехполюсники
Сложные четырехполюсники можно представить в виде различных соединений простых четырехполюсников. При этом параметры сложного четырехполюсника могут быть найдены по параметрам образующих его простых четырехполюсников.
В зависимости от способа соединения для определения параметров сложных четырехполюсников применяются различные формы уравнений:
1) при каскадном соединении – форма или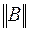 
;
2) при последовательном соединении – форма 
;
3) при параллельном – форма 
.
Каскадное соединение
Каскадным называют такое соединение четырехполюсников, при котором входные зажимы каждого последующего четырехполюсника присоединяются к выходным зажимам предыдущего (рис. 9.14).
Для каждого четырехполюсника можно записать систему уравнений в матричном виде:
и 
.
Из рис. 9.14 видно, что выходной ток первого четырехполюсника является входным током второго четырехполюсника и выходное напряжение первого четырехполюсника является входным напряжением второго, то есть
.
Это приводит к тому, что матрицы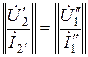 
равны между собой. Подставляя 
вместо 
, для результирующего четырехполюсника получим:
.
Таким образом, матрица результирующего четырехполюсника при каскадном соединении равна произведению матриц коэффициентов составляющих четырехполюсников. Это правило распространяется на любое число составляющих, но при умножении матрицы должны записываться в порядке следования четырехполюсников, так как умножение матриц не подчиняется переместительному закону.
