Входное сопротивление линии, измеренное в произвольной точке на расстоянии х' от конца, определяется отношением Z=U/I и может быть представлено в комплексной или гиперболической форме. Будем считать, что линия нагружена на конце некоторым сопротивлением Z2, которое в зависимости от условий может быть любым.
На основании системы уравнений комплексное входное сопротивление линии
Данное выражение показывает, что с изменением координаты х' модуль входного сопротивления линии колеблется между некоторыми максимумами и минимумами (которые в общем случае отличаются друг от друга).
Допустим, что модуль Z дocтигaeт некоторого максимума в точке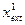 
. Тогда максимумы будут также в точках, соответствующих изменению аргумента 2 
х' на 2 
, что дает
Следовательно, максимумы чередуются через каждые полволны. Посередине между максимумами будут минимумы, которые также чередуются через каждые пол волны.
Если вместо координаты х' варьировать коэффициент фазы 
, меняя частоту источника, получится аналогичная волнообразная кривая, причем максимумы и минимумы будут отстоять друг от друга на 
/х' (здесь х' = const). Исследуя изменение входного сопротивления линии при плавном изменении частоты источника, можно зафиксировать два следующих друг за другом максимума сопротивления Z, соответствующих частотам 
и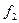 
. В этом случае 
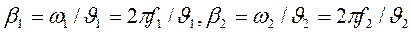и, следовательно, 
откуда 
При малом расхождении частот f1 и f2 фазовые скорости почти одинаковы: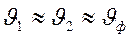 
, а 
. Данная формула позволяет определить расстояние от точки наблюдения до ближайшей точки линии, в которой имеет место отражение (например, при коротком замыкании на линии), произведя измерение только в одной точке.
Так как коэффициент фазы 
определяется по формуле (17.46) неоднозначно, то проверка расчетов проводится с использованием формулы (17.14), причем первоначально фазовая скорость 
выбирается ориентировочно.
На рис. 17.11 показаны кривые изменения модулей Zx и ZK в зависимости от координаты х'. В пределе, т.е. при х' -» оо, максимумы и минимумы кривой стремятся к значению 
.
Входные сопротивления линии без потерь при холостом ходе и коротком замыкании могут быть рассчитаны по формулам (17.44) и (17.45) при замене 
; 
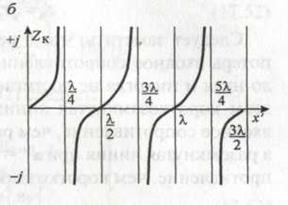
Эти реактивные входные сопротивления с учетом их знака изображаются отангенсоидами и тангенсоидами соответственно (рис. 17.12). Аргументом может служить также величина 
, если изменять частоту при постоянной длине х'.
Входное сопротивление линии без потерь при х' 
4 носит индуктивный характер в режиме короткого замыкания и емкостный в режиме холостого хода. При х' = 
/4 в первом случае наступает резонанс токов (z =oo), во втором - резонанс напряжений (z=0).
Согласно уравнению (17.42), входное сопротивление линии без потерь, нагруженной произвольным сопротивлением 
,
где Ф — аргумент комплексного коэффициента отражения 
Входное сопротивление линии достигает максимума при 
, или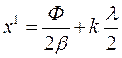 
На основании формул (17.48) и (17.49) волновое сопротивление линии без потерь может быть определено как среднее геометрическое максимального и минимального значений входного сопротивления линии: 
Следует заметить, что в реальных условиях при наличии потерь входное сопротивление линии никогда не снижается до нуля и никогда не достигает бесконечного значения. При этом короткозамкнутая линия при х' 4 имеет большее входное сопротивление, чем разомкнутая линия при х' 
2, а разомкнутая линия при х' 4 имеет меньшее входное сопротивление, чем короткозамкнутая при х' 2
