Независимо от того, соблюдается ли условие 
(для неискаженной передачи требуется, чтобы коэффициент ослабления 
не зависел от частоты, а коэффициент 
был прямо пропорционален частоте; в последнем случае фазовая скорость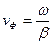 
получается не зависящей от частоты, такое положение имеет место при условии, что 
.) или нет, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).
В воздушных линиях обычно индуктивное сопротивление 
превышает активное сопротивление r, а емкостная проводимость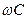 
превышает активную проводимость g. С ростом частоты разница между этими величинами становится более значительной.
В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т.е. пренебрегать активным сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.
Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, является приближенное условие, что 
и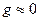 
, в этом случае вторичные параметры линии примут весьма простой вид, а именно: 
; 
; 
; 
Следовательно в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости 
отсутствуют также фазовые искажения.
Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений (вопрос 57). Следовательно, все что сказано о линии без искажений, относится к линии без потерь.
Уравнения линии в показательной форме:
Уравнения линии в гиперболической форме -à:
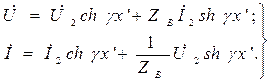
Положив в этих уравнениях, что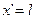 
, получим уравнения линии в гиперболической форме, выражающие напряжения и ток в начале через напряжения и ток в конце:
Ввиду того что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии принимают тригонометрическую форму:
Последние уравнения используются для рассмотрения стоячих волн.
Пользуясь уравнениями линии в комплексной и гиперболической формах рассмотрим систему, где мнимый коэффициент распространения примем равным 
,получим для любой точки линии на расстоянии x’ от конца:
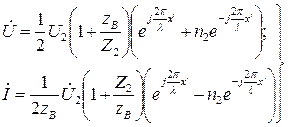
Входящий в эти уравнения коэффициент отражения
представляет в общем случае комплексную величину. Эти уравнения показывают, что в любой точке x’ слагается из падающей и отраженной волн напряжения, амплитуды которых находятся в отношении 1:|n2|; в свою очередь комплексный ток равен разности падающей и отраженной волн тока с тем же соотношением амплитуд. Точкам 
, соответствует максимально действующее значение U, так как при этом фазы падающей и отраженной волн напряжения совпадают. На расстоянии 
от этих точек падающая и отраженная волны оказываются в противофазе и действующее напряжение имеет минимум.
Координаты максимумов и минимумов U, являющиеся функциями от 
и 
не зависят от времени, т.е. с течением времени остаются на одном месте.
При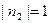 
,т.е. при равенстве амплитуд прямой и обратной волны, в лини устанавливаются стоячие волны напряжения и тока. Кривые действующих U и I вдоль линии представляют в этом случае “выпрямленные” синусоиды. На линии образуются узлы – точки где U и I равны нулю, и пучности – где U и I максимальны.
Условие 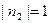выполняется в трех случаях: при 
(холостой ход), 
(короткое замыкание), и при 
(реактивная нагрузка). Это для линий без потерь.
Стоячие волны легко исследуются с помощью уравнений для линии без потерь:
При холостом ходе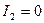 
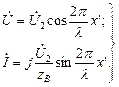
Узлы напряжения находятся в очках, для которых 
, откуда 
.
Пучности напряжения находятся в точках, для которых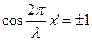 
, откуда 
Разомкнутый конец линии совпадает с узлом тока и пучностью напряжения.
При коротком замыкании 
:
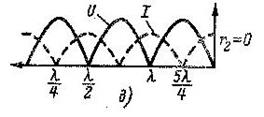
На замкнутом конце линии x’=0 и в точках, удаленных от него на целое число полуволн 
, находятся узлы напряжения и пучности тока, а в точках, удаленных от конца на нечетное число четвертей волн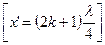 
, находятся пучности напряжения и узлы тока.
