Переходной характеристикой 
называется уравнение, составленное для участка цепи или для всей в це 
лом, которое описывает переходный процесс, если цепь подсоединяется к источнику с постоянным входным сигналом равным 1 (1А или 1В).
– переходная характеристика для тока
– переходная характеристика для напряжения
– переходное сопротивление
– переходная проводимость
Переходная проводимость – реакция электрической цепи, численно равной току при воздействии на эту цепь единичной ступенчатой функции напряжения.
, т.к 
, то 
, (1)
, (2)
Переходная функция напряжения - это реакция электрической цепи, численно равная напряжению при воздействии на эту цепь единичной ступенчатой функции напряжения.
Переходная функция тока - реакция цепи, численно равной току при воздействии на эту цепь единичной функции тока.
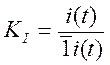
Переходное сопротивление – реакция электрической цепи в виде напряжения при воздействии единичной ступенчатой функции тока.
Каким бы не было заданное входное воздействие или ток источников, его принимают равным 1В или 1А.
1) Определяют ННУ 
и 
и т.д. т.е. для полученной цепи рассчитываем п/пр. любым методом. Полученные уравнения для 
и 
дадут соответствующие переходные характеристики.
Пример.
Найти переходную характеристику по току для цепи
для ветви с сопротивлением 
при воздействии на входе ИТ 
, 
.
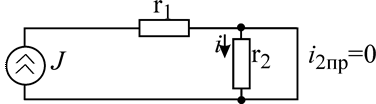
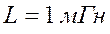Решение
1) 
2) ННУ 
3) 
4) 
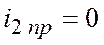
5) 
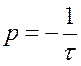, где 
, 
, 
.
6) ЗНУ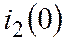 
наедем из после коммутационной схемы:
7) Полное решение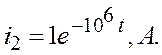 
8) Переходное характеристика безразмерна:
30.Интеграл Дюамеля.
– все время действия функции. Этот разбиваем на элементарные скачки и заменяем приближенной ступенчатой функцией.
При достаточно малом 
реакция цепи на первый прямоугольный импульс приближенно равна реакции цепи на единичную функцию помноженную на высоту первой ступени: 
. Реакция цепи на вторую ступень: 
, где 
- высота второй ступени;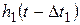 
- реакция цепи на единичную функцию, смещенную в сторону запаздывания на 
и т.д.
Следовательно, для рассматриваемого момента времени 
реакция цепи 
равна:
При 
и 
-это первая форма записи интеграла Дюамеля, т.е. выходной сигнал:
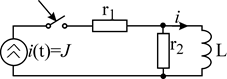
Расчет переходных процессов методом интеграла Дюамеля. Рассмотреть на примере.
R=2 Ом L=5 мГн
На входе непериодические несинусоидальные сигналы
Общая формула интеграла Дюамеля:
Для нашего случая
Переходная проводимость g(t) есть реакция цепи на единичное ступенчатое воздействие.
Подадим на вход единичное напряжение, на выходе получим единичный ток:
Схема:
Ток Ir(t) будет равен проводимости переходной характеристики.
Найдём этот ток.
1.ННУ: 
2. Установившийся режим: 
.
3. Свободный режим: 
4.ЗНУ:
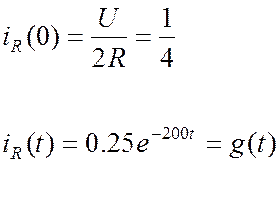
в итоге получаем ток:
