Характеристическое уравнение имеет вид:
ri+L 
=E
Lp+r=0
p=-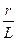 
Для определения вида свободной составляющей необходимо составить и решить характеристическое уравнение: z(p)=0.Для записи характеристического уравнения необходимо нарисовать схему,в которой все источники ЭДС и тока следует заменить на их же внутреннее сопротивление,а сопротивление индуктивности и емкости принять соответственно равным Pl и 
,далее необходимо разорвать любую ветвь данной схемы,записать ее исходное сопротивление относительно точек разрыва,прировнять его нулю,решить и определить корни p,если корни получились действительными отрицательными,то своб.составляющая искомой функции:
,где m-количество корней уравнения;
-корни; 
-постоянные интегрируемые.
Если корни характер.уравнения получились комплексно сопряженными,то своб.сост.будет иметь вид:
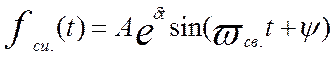где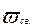 
-частота свободных колебаний;
-начальная фаза свободных колебаний.
8.Время переходного процесса. Определение практически tпп. Расчет времени переходного процесса.
Время переходного процесса зависит от коэфициента затухания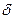 
.Величина,обратная 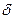,называется постоянной времени 
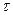и представляет собой время,в течении которого значение свободной составляющей переходного процесса уменьшится в e=2,72 раза. Величина 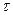зависит от схемы и параметров.Так для цепи с последовательным соединением r и L = 
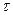,а при последовательном соединениии
R и 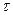C =Rc.
95% окончания переходного процесс 3 .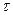
Кривые свободных составляющих переходного процесса проще всего построить, задавая времени t значения 0, 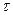,2 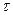…..Если вещественных корней несколько,то результирующая кривая получается путем суммирования ординат отдельных слагаемых (рис.1.)
Рисунок 1:
9.10,Переходный процесс в r, С – цепи при включении на источник постоянного напряжения. Анализ произвести классическим методом; привести аналитические выражения для UC(t); iC(t); графики. (Классический метод).
Уравнение состояния rC-цепи после коммутации следующее:
(1),или rC 
(2)
Его решение: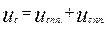 
Емкость С после замыкания ключа при t 
зарядится до установившегося значения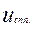 
.Свободная составляющая 
Поскольку начальные условия нулевые,согласно закону коммутации 
при t=0,или 0=A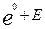 
,откуда A=-E.
Решение уравнения (2) примет вид:
+E=E(1- )
где 
=rC
Ток в цепи i(t)=C 
Рисунок 1.
Рисунок 2.
Графики изменения напряжения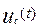 
и тока i(t) приведены на рисунке 1 и 2. Из рисунков видно,что напряжение 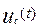на конденсаторе возростает по экспоненциальному закону от 0 до E,сила тока же в момент коммутации скачком достигает значения E/r, а затем убывает до нуля.
11.12.Переходный процесс в r, C – цепи при подключении к источнику синусоидального напряжения. Анализ произвести классическим методом; привести аналитические выражения для UC(t); iC(t); графики. (Классический метод).
Уравнение состояния rC-цепи в переходном режиме следующее
rC 
.
Решение этого уравнения:
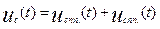
Свободная составляющая
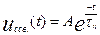где =rC
Так цепь линейна,то при синусоидальном воздействиии в установившемся режиме напряжение на емкости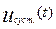 
также будет изменяться по синусоидальному закону с частотой входного воздействия,Поэтому для определения 
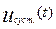= воспользуемся методом комплексных амплитуд:
; 
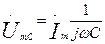где 
= 
;
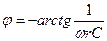
Учитывая, что j= 
,получаем:
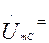
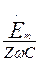
откуда
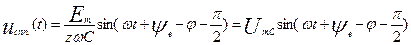
Постоянную интегрирования А свободной составляющей
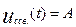
найдем из начальных условий в цепи с учетом закона коммутации:
.При t=0 последнее выражение имеет вид
0=A+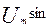 
Откуда A=-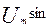
Cложив составляющие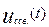 
и 
,получим окончательное выражение для напряжения на емкости в переходном режиме:
= + = 
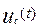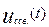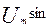
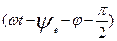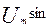
- (1)
Анализ выражения (1) показывает, что переходный процесс в rC-цепи при синусоидальном воздействии зависит от начальной фазы ЭДС источника в момент коммутации и от постоянной времени rC-цепи.
Если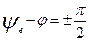 
,то 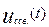=0 и в цепи сразу после коммутации наступит установившийся режим,т.е.
= = 
.
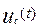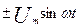При 
напряжение =-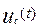 
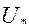
, т.е. напряжение на емкости сразу после коммутации может достигать почти удвоенного значения 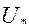положительного знака,а затем постепенно приближаться к = .
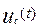Разность фаз 
приведет уравнение (1) к виду:
= 
.
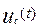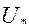
Отличие данного режима от предыдущего состоит в том,что напряжение на емкости сразу после коммутации может достичь почти удвоенного значения 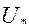отрицательного знака.
Для расмотренной Rc-цепи с источником синусоидального тока в установившемся режиме начальная фаза входного напряжения никакой роли не играет, но в переходном процессе ее влияние существенно.
13.Переходный процесс в r, L, C – цепи при подключении к источнику постоянного напряжения. Периодический процесс. Аналитические выражения для i(t), графики. (Классический метод).
Uc(0-)=Uc
Il(j-)=0
Корни действительные, отрицательные, разные.
I(t)=Iуст+A1ep1t+A2ep2t
Процесс периодический:
t=0 {i(0)=A1+A2; A1=-A2
{ 
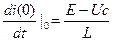
t=0 il(0)*r+L 
+Uc(0)=E A1=-A2=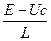 
(
)
il(t)= (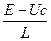
)
il(t)= (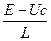
)
14.Переходный процесс в r, L, C – цепи при подключении к источнику постоянного напряжения. Критический процесс. Аналитические выражения для i(t), графики. (Классический метод).
p1=p2=-δ= 
il(t)=iуст+(B1+B2*t)*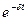 
t=0: il(0)=β1=0
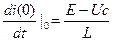
il(t)= ()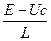
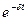Если корни получились действительные, отрицательные, равные, значит процесс критический.
15.Переходный процесс в r, L, C – цепи при подключении к источнику постоянного напряжения. Колебательный процесс. Аналитическое выражение для i(t), графики. (Классический метод).
Pt= -δ±j*ωсв ωсв= 
Корни отрицательные действительные, частью комплексносопряженные.
il(t)=iустA1e-δt*sin(ωсвt+ψ)
il(t)=iуст+(M*cos ωсв t+N*sin ωсв t)*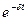
il(t)= 
* 
= 
* 
При δ→0
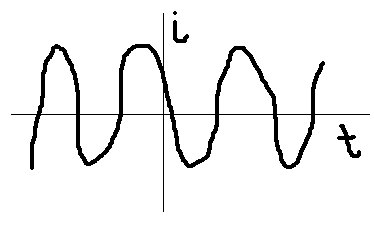
16. Переходный процесс в r, L, C – цепи при подключении к источнику синусоидального напряжения. Апериодический процесс. Аналитическое выражение для i(t), графики. (Классический метод).
R(t)=Emax*sin(ωt+ψ)
1.Н.Н.У
Uc(0)=Uc
il(0)=0
2. 
φ=arctg 
Iуст=imax*sin(ωt+ψ-φ)
t=0
il(t)= iуст(t)+iсв(t)
при Туст<ТАУ
при Туст≈ТАУ
при Туст>ТАУ
17.Переходный процесс в r, L, C – цепи при подключении к источнику синусоидального напряжения. Колебательный процесс. Математическое описание i(t), графики. (Классический метод).
R(t)=Emax*sin(ωt+ψ)
1.Н.Н.У
Uc(0)=Uc
il(0)=0
2.
φ=arctg
Iуст=imax*sin(ωt+ψ-φ)
t=0
il(t)= iуст(t)+iсв(t)
При Туст>Tα
При Туст≈Tсв
При Туст<Tсв
