Справжня вартість грошей при використанні складної процентної дисконтної ставки визначається по формулі:
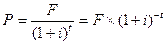, (3.39)
де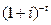 
- дисконтний множник;
і - складна процентна дисконтна ставка.
У фінансових обчисленнях базова формула (39) визначення справжньої вартості може бути трансформована з урахуванням різних періодів формування грошових потоків:
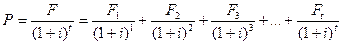(3.40)
де F1, F2, F3, …Ft - майбутня вартість грошей, що формується по періодах;
(1 +i)1, (1 +i)2, (1 +i)3 , …, (1 +i)t - дисконтні множники по періодах;
t - число періодів, приведення майбутньої вартості до справжнього моменту часу.
Запропонована формула є базовою для оцінки ефективності інвестиційних проектів. Щоб оцінити ефективність інвестиційного проекту у формулу 40 необхідно внести невеликі доповнення, що припускають зменшення справжньої приведеної вартості на величину стартових інвестицій. Формула для розрахунку може бути:
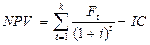, (3.41)
де NPV – чиста приведена вартість;
ІС - стартові інвестиції.
При нарахуванні складних дисконтних відсотків (m) раз на рік формулу 39 можна представити у такому вигляді:
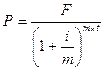, (3.42)
де 
- дисконтний множитель.
Для формул 39 і 42 значення дисконту може бути визначено по наступним формулам:
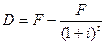, (3.43)
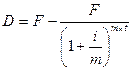, (3.44)
Задача 22.
Векселедержатель надав для обліку вексель на суму 2,6 млн. грн. з терміном погашення 1 лютого поточного року. Вексель пред'явлено 12.01 поточного року. Банк погодився врахувати вексель з дисконтом 16% річних. Визначити суму, яку отримає векселедержатель і суму дисконту, отриману банком.
Задача 23.
Підприємство продало товар в кредит з оформленням простого векселя, номінальна вартість якого 470 тис. грн., термін векселя - 65 днів, ставка відсотка за кредит - 20% річних. Через 45 днів з моменту оформлення векселя підприємство вирішило врахувати вексель в банку; запропонована банком дисконтна ставка склала 16% річних. Визначити суми, отримані підприємством і банком в результаті даної операції.
Методичні вказівки до розв’язання задачі 22, 23.
При банківському методі визначення справжньої приведеної вартості грошей при простій обліковій дисконтній ставці розрахунок проводиться по формулі:
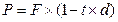(3.45)
де d - облікова дисконтна ставка, долі одиниць.
Справжня вартість грошей при складній дисконтній обліковій ставці визначається по формулі:
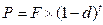(3.46)
де d - складна річна дисконтна облікова ставка.
Дисконт обчислюється за формулою:
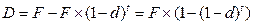(3.47)
Складна дисконтна облікова ставка може бути визначена по формулі:
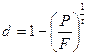(3.48)
Задача 24.
Рентні платежі виплачуються протягом 5 років у розмірі 14 тис. грн. Процентна ставка 16% річних. Визначити майбутню вартість ануїтету за наступних умов:
а) платежі вносяться один раз до року, а відсотки нараховуються щоквартально;
б) платежі вносяться 2 рази до року рівними сумами, а відсотки нараховуються один раз в рік;
в) рентні платежі вносяться щоквартально, відсотки нараховуються щоквартально;
г) рентні платежі вносяться щокварталу, а відсотки нараховуються по півріччям.
