Каждой обобщенной координате соответствует обобщенный импульс:

Рассмотрим функцию  :
:

перейдем от  к
к 
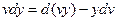


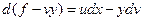


Здесь  - функция переменных
- функция переменных  и
и 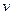 .
.  - отсюда находим
- отсюда находим  . Это и есть преобразование Лежандра.
. Это и есть преобразование Лежандра.
Рассмотрим функцию Лагранжа  . От
. От  и
и  перейдем к
перейдем к  и
и  :
:


 - обобщенный импульс
- обобщенный импульс
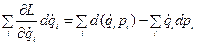


используя уравнение Лагранжа  , получим:
, получим:
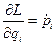
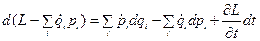
Мы перешли к переменным  ,
,  ,
,  . По определению:
. По определению:
 - функция Гамильтона.
- функция Гамильтона.
Выразим  через
через  и
и  . Из
. Из  получаем
получаем  . Запишем
. Запишем  :
:


Сравнивая два этих выражения, получаем:


Это уравнения движения Гамильтона, их так же называют каноническими. Их  штук. В отличие от
штук. В отличие от  дифференциальных уравнений Лагранжа, которые были 2-го порядка, эти
дифференциальных уравнений Лагранжа, которые были 2-го порядка, эти  дифференциальных уравнений первого порядка. Для решения
дифференциальных уравнений первого порядка. Для решения  уравнений надо задать
уравнений надо задать  начальных условий, или
начальных условий, или  динамических переменных в какой-то момент времени:
динамических переменных в какой-то момент времени: 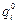 и
и  .
.  и
и  - динамические переменные в методе Гамильтона.
- динамические переменные в методе Гамильтона.
Обратимся к равенству  . Величины
. Величины  и
и  называют канонически сопряжёнными величинами (по Гамильтону). Канонические преобразования в методе Гамильтона служат для перехода от одних динамических переменных к другим.
называют канонически сопряжёнными величинами (по Гамильтону). Канонические преобразования в методе Гамильтона служат для перехода от одних динамических переменных к другим.
Функцию Гамильтона можно также получить ещё с помощью вариационного метода.
Фазовое пространство.
В методе Гамильтона рассмотрим  мерное пространство, где по осям откладываются переменные
мерное пространство, где по осям откладываются переменные  , это и есть фазовое пространство. Точка в нём – фазовая точка. Здесь каждая точка описывает определённое динамическое состояние системы. При движении системы, фазовая точка описывает траекторию, называемую фазовой траекторией.
, это и есть фазовое пространство. Точка в нём – фазовая точка. Здесь каждая точка описывает определённое динамическое состояние системы. При движении системы, фазовая точка описывает траекторию, называемую фазовой траекторией.

Функция Гамильтона и её свойства.

Функция Лагранжа задаётся неоднозначно, т.е.
 , где
, где 
приводят к одним и тем же уравнениям движения.
То же самое справедливо и для функции Гамильтона:
 , где
, где 
Функция Гамильтона простейших систем.
1. Свободная материальная точка:
Ее потенциальная энергия равна нулю, тогда 
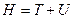

Получим  для данного случая:
для данного случая:

Используем  , тогда получим:
, тогда получим:


2. Система  свободных материальных точек:
свободных материальных точек:


3. Замкнутая система  материальных точек
материальных точек
 , где
, где 

4.  материальных точек во внешнем поле:
материальных точек во внешнем поле:

5.  материальных точек в стационарном внешнем поле:
материальных точек в стационарном внешнем поле:
 - зависит только от
- зависит только от 
Отличие 5-го и 3-го случая заключается в том, что в 5-м случае  -составляющая во внешнем поле, она аддитивна -
-составляющая во внешнем поле, она аддитивна -  ; если взаимодействие частиц с внешним полем одинаково, то
; если взаимодействие частиц с внешним полем одинаково, то  .
.
6. Замкнутая система двух материальных точек:


в силу однородности и изотропности пространства можем записать:

Задачи
1. Найти функцию Гамильтона для одной материальной точки в декартовых, цилиндрических и сферических координатах.
Решение. В декартовых координатах x, y, z:
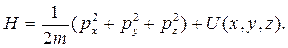
В цилиндрических координатах r, φ, z:
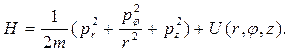
В сферических координатах r, θ, φ:







