Теоретическая механика и теория поля
(конспект лекций для ЭКТ-2)
Г.
§1. Обобщённые координаты. Понятие числа степеней свободы........................................................ 4
§2. Описание эволюции системы в конфигурационном пространстве (КП)..................................... 5
§3. Принцип Гамильтона (наименьшего действия)................................................................................ 6
§4. Функция Лагранжа и её свойства........................................................................................................ 7
§5. Правило суммирования Эйнштейна................................................................................................... 7
§6. Функция Лагранжа простейших систем............................................................................................. 8
§7. Интегралы движения в методе Лагранжа........................................................................................ 11
§8. Преобразование Галилея..................................................................................................................... 11
§9. Свойства симметрии пространства и времени............................................................................... 11
§10. С и l системы........................................................................................................................................ 13
§11. Циклические координаты.................................................................................................................. 14
§12. Задача двух тел и сведение её к эквивалентной одномерной...................................................... 14
§13. Особенности движения частицы в центральном поле................................................................. 16
§14. Одномерный эффективный потенциал........................................................................................... 17
§15. Обобщенный импульс. Преобразование Лежандра. Уравнения Гамильтона........................ 17
§16. Фазовое пространство........................................................................................................................ 19
§17. Функция Гамильтона и её свойства................................................................................................ 19
§18. Функция Гамильтона простейших систем..................................................................................... 19
§19. Интегралы движения в методе Гамильтона.................................................................................. 21
§20. Скобки Пуассона и их свойства........................................................................................................ 21
§21. Малые колебания и свойства потенциальной энергии............................................................... 25
§22. Колебания с одной степенью свободы. Характеристическое уравнение................................. 25
§23. Колебания с n степенями свободы................................................................................................... 28
§24. Затухающие одномерные колебания............................................................................................... 34
§25. Элементы тензорного анализа в классической механике........................................................... 35
§26. Оператор 
.......................................................................................................................................... 37
§27. Уравнения Максвелла для электромагнитного поля в вакууме............................................... 38
§28. Потенциалы электромагнитного поля в вакууме......................................................................... 38
§29. Градиентная инвариантность........................................................................................................... 38
§30. 
-функция........................................................................................................................................... 39
§31. Объёмная плотность точечного заряда........................................................................................... 40
§32. Закон сохранения заряда.................................................................................................................... 41
§33. Типы калибровок................................................................................................................................ 41
§34. Уравнения Максвелла в среде без учёта пространственно-временной дисперсии................ 44
§35. Теорема Стокса.................................................................................................................................... 45
§36. Функциональные соотношения различных полей....................................................................... 46
§37. Тензоры 
и их свойства............................................................................................................ 47
§38. Условия на границе раздела двух сред............................................................................................ 48
§39. Уравнения Максвелла для стационарного электромагнитного поля в среде........................ 51
§40. Приближение линейного тока........................................................................................................... 53
§41. Уравнения Максвелла для квазистационарного электромагнитного поля............................ 54
§42. Условия квазистационарности поля............................................................................................... 55
§43. Глубина проникновения квазистационарного электромагнитного поля................................ 56
§44. Функция Грина уравнения Гельмгольца....................................................................................... 57
§45. Уравнения Максвелла электромагнитных волн в вакууме....................................................... 58
§46. Волновое уравнение в случае вакуума........................................................................................... 59
§47. Решение волнового уравнения в случае плоской электромагнитной волны в вакууме...... 59
§48. Плоская монохроматическая волна................................................................................................ 61
§49. Уравнения Максвелла в случае плоской монохроматической волны в вакууме.................. 61
§50. Разложение электромагнитных полей по плоским монохроматическим волнам.................. 62
§51. Калибровка Лоренца в случае однородной изотропной среды.................................................. 62
Задачи по курсу «Теоретическая механика и теория поля»............................................................... 63
Задачи по курсу «Теоретическая механика и теория поля» и их решение...................................... 68
Экзаменационные вопросы по курсу «Теоретическая механика и теория поля».......................... 74
Задачи по курсу «Теоретическая механика и теория поля» и их решение (от А.Е.Широкова).. 76
Обобщённые координаты. Понятие числа степеней свободы.
Пусть число степеней свободы равно 
. Для задания пространственного положения системы необходимы координаты.
– размерность пространства.
– число материальных точек.
числу координат, с помощью которых можно задать положение материальных точек.
– радиус вектор а-той точки.
Если имеются связи, т.е. ограничения, накладываемые на движение системы, причём выраженные в форме уравнений, содержащих эти координаты, то число независимых координат будет меньше на число этих связей.
- все радиус векторы.
, 
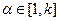, где k – число связей.
Такие связи называются голономными. Если присутствует время (t) в уравнениях, то связи – нестационарные.
Для вычисления числа степеней свободы можем записать формулу:
Любые независимые переменные, полностью определяющие пространственное положение системы, называются обобщёнными координатами.
Виды координат:
Сферические 
.
Декартовы 
.
И другие.
Графическое пояснение:
Вывод данных формул элементарен по Рис.1
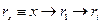- i -тая компонента.
Рассмотрим пример:
Дан математический маятник (Рис.2). 
- это n-мерный вектор. Здесь n=1, 
и уравнения связи имеют вид:
где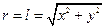 
.
- уравнение связи.
Определим число степеней свободы:
Тогда число степеней свободы равно единице.
