 , где
, где  -
-  -мерный вектор.
-мерный вектор.

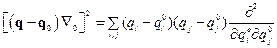


В точке  - экстремум(минимум):
- экстремум(минимум):

 - условие минимума, оно понимается в смысле квадратичных форм, т.е. если умножить на вектор слева и на вектор справа, то образуется положительная скалярная величина:
- условие минимума, оно понимается в смысле квадратичных форм, т.е. если умножить на вектор слева и на вектор справа, то образуется положительная скалярная величина:
 , для
, для 
 , где
, где 

Тогда функция Лагранжа имеет вид:

она описывает малые свободные гармонические колебания.

Уравнение движения для данной системы:
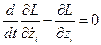
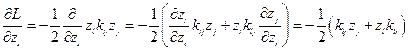


Аналогично можно получить:
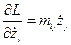

Подставим полученные формулы в уравнение движения, тогда получим:


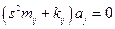 - система линейных однородных дифференциальных уравнений.
- система линейных однородных дифференциальных уравнений.
Эта система имеет нетривиальное решение, если:
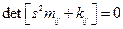 - дисперсионное уравнение
- дисперсионное уравнение
Это матрицы 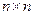 с действительными коэффициентами.
с действительными коэффициентами.
 имеет
имеет  решений
решений  ,
, 
 , где
, где 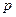 - номер корня.
- номер корня.

умножим это выражение на  и просуммируем:
и просуммируем:
 ,
, 


Получаем:
 -матричное уравнение
-матричное уравнение
пусть 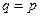 :
:
 ,
, 
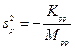
т.к.  , тогда:
, тогда:

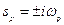
Из определения матриц  и
и 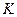 следует, что
следует, что

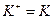
Можно показать, что 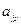 - вещественные числа, тогда
- вещественные числа, тогда 

 т.е. матрицы симметричные, значит:
т.е. матрицы симметричные, значит:
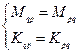 (23.1)
(23.1)
Запишем два матричных уравнения:


воспользуемся свойством (23.1) и сложим два этих уравнения:

т.к. корни различны, то при  получаем
получаем 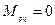 .
.
Если  , то
, то  , но она неопределённая. Эта неопределённость исключается нормировкой:
, но она неопределённая. Эта неопределённость исключается нормировкой:
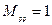
Эта нормировка позволяет найти неопределённый параметр  для всех корней.
для всех корней.
Таким образом:
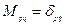
Рассмотрим матрицу 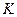 :
:

тогда:
 , где
, где 
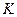 -диагональная матрица.
-диагональная матрица.
Тогда  - преобразование с помощью которого
- преобразование с помощью которого  переводится в единичную, а
переводится в единичную, а 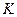 диагонализируется.
диагонализируется.

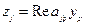 , где
, где 
Тогда:
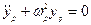
Переменные  - нормальные координаты, или главные колебания. Это простейшая форма колебаний.
- нормальные координаты, или главные колебания. Это простейшая форма колебаний.
 - комплексная константа.
- комплексная константа.
 и
и  находятся из начальных условий:
находятся из начальных условий:

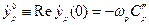
 , и
, и 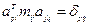 , т.е.
, т.е.  - единичная матрица.
- единичная матрица.

для того чтобы получить единицу перед  надо левую и правую часть умножить на
надо левую и правую часть умножить на  :
:
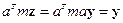


Для компоненты  :
:
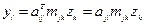
Начальные условия:


Схема решения задач:
1. Составить дисперсионное уравнение.
2. решаем, находим корни(собственные частоты)
3. находим решения для нормальных координат
4. из решения уравнений находим коэффициент  :
:


 находим матрицу,
находим матрицу,  искомый коэффициент.
искомый коэффициент.
5. зная  и
и 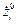 находим
находим  и
и 
6. через 3. находим 
7. находим 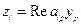






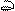

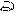


 Рассмотрим колебательный LC-контур
Рассмотрим колебательный LC-контур
 ,
, 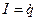
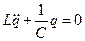
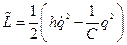 - функция Лагранжа для данной системы.
- функция Лагранжа для данной системы.
 |
Рассмотрим контур
 - энергия, связанная с наличием индуктивности в системе,
- энергия, связанная с наличием индуктивности в системе,


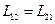
Энергия, связанная с конденсатором  ,
,
 - емкости
- емкости
 - электростатическая индукция
- электростатическая индукция

Задачу эту необходимо упрощать.
Рассмотрим задачу:
Свободные колебания двухатомной молекулы.

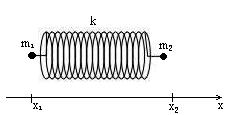 - коэффициент взаимодействия.
- коэффициент взаимодействия.
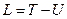
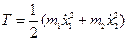

здесь  - удлинение по сравнению с равновесным состоянием пружины.
- удлинение по сравнению с равновесным состоянием пружины.
 ,
,  - координаты точек в отсутствии деформации пружины.
- координаты точек в отсутствии деформации пружины.
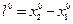
 ,
,  - координаты точек в деформированном состоянии
- координаты точек в деформированном состоянии


Можем найти потенциальную энергию.
Вводим переменные 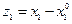 и
и 


Найдём  и
и  :
:
 и
и 
1. Составим дисперсионное уравнение:


Решая его получим два корня:
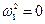 и
и 
2. Напишем дифференциальные уравнения для нормальных колебаний:
 - здесь колебаний нет, т.к.
- здесь колебаний нет, т.к. 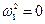
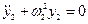
 , где
, где 
3. Найдём матрицу  .
.
Используем уравнения: 
Пусть  , тогда:
, тогда:


значит  .
.



Аналогично рассуждая для 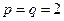 получим:
получим:

и из условия нормировки:
 , где
, где 
тогда:
 ,
, 
 ,
,  , но
, но  - диагональная, тогда:
- диагональная, тогда:
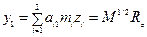
Здесь  - координата центра масс
- координата центра масс
Рассуждая аналогично для  , получим:
, получим:
 , где
, где 
Пусть  ,
,  ,
,  , тогда:
, тогда:
 и
и 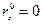
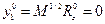




 , тогда
, тогда 



Подставляя сюда выражения для  и
и  получим:
получим:

Итак, решение задачи:


Задачи
1. Определить малые колебания двойного плоского маятника.
 |
Решение. Для малых колебаний
 найденная в задаче 1 параграфа 6 функция Лагранжа принимает вид:
найденная в задаче 1 параграфа 6 функция Лагранжа принимает вид:
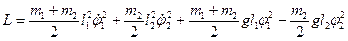 .
.
Уравнения движения:

После подстановки (23,6):


Корни характеристического уравнения:
Ответ:  .
.
При  частоты стремятся к пределам
частоты стремятся к пределам 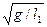 и
и  , соответствуют независимым колебаниям двух маятников.
, соответствуют независимым колебаниям двух маятников.






