коэффициент вариации; 3) t – статистика;
коэффициент детерминации; 4) F – критерий.
2. Какой показатель тесноты связи изменяется в пределах от -1 до +1?
эмпирическое корреляционное отношение; 2) коэффициент детерминации; 3) парный коэффициент корреляции; 4) коэффициент эластичности.
Как рассчитывается парный коэффициент корреляции?
1) 
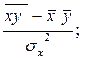2) 
3) 
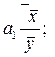4) 
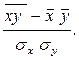
Какая задача решается при определении коэффициента детерминации?
оценка тесноты и направления связи; 2) оценка тесноты связи; 3) какая часть вариации у зависит от вариации х? 4) эластичность изменения у от изменения х.
На основе какого соотношения проверяется статистическая однородность распределения факторного признака?
1) коэффициента корреляции; 3) корреляционного отношения;
2) коэффициента вариации; 4) коэффициента эластичности.
6. Какие характеристики не относятся к параметрическим показателям тесноты связи:
1) коэффициент Фехнера; 3) коэффициент ранговой корреляции;
2) коэффициент конкордации; 4) корреляционное отношение.
7. Для взаимосвязи между альтернативными признаками применяется:
коэффициент взаимной сопряженности; 2) коэффициент контингенции; 3) коэффициент конкордации; 4) коэффициент корреляции
8. Какой показатель рассчитывается по формуле: 
парный коэффициент корреляции; 2) коэффициент детерминации; 3) коэффициент эластичности; 4) частный коэффициент корреляции.
Какой показатель применяется для оценки уровня статистической точности уравнения связи?
1) t -критерий; 2) F –критерий; 3)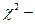 
критерий; 4)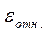 
Решение типовых задач
Пример 1. По итогам аналитической группировки, изучающей зависимость средней заработной платы рабочих от возраста (пример 6 темы 5) с помощью однофакторного дисперсионного анализа: 1) проерить статистическую существенность зависимости; 2) оценить тесноту связи между средней заработной платой и возрастом.
Решение
1. Для проверки статистической существенности зависимости между изучаемыми факторами строим однофакторный дисперсионный комплекс (табл.10.6), предварительно рассчитав соответствующие девиации и дисперсии:
+ 
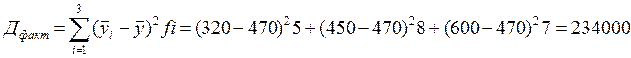
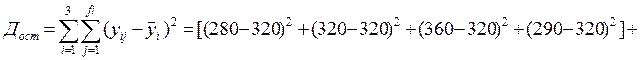
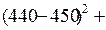
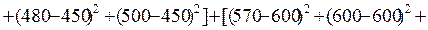
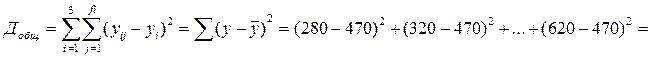
= 269000.
Таким образом, выполняется правило разложения вариации:
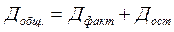, или 269000 = 234000 + 3500.
Определяем число степеней свободы для каждого вида девиации: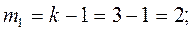 
.
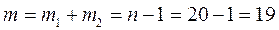Тогда соответствующие дисперсии будут равны:
факторная: 
; остаточная: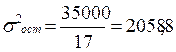 
;
общая: 
.
По соотношению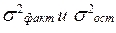 
рассчитывается F- критерий:
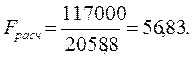Итоговые значения рассчитанных характеристик представим в таблице 10.6.
Таблица 10.6
Однофакторный дисперсионный комплекс зависимости средней заработной платы от возраста рабочих
| Источник вариации | Девиа ция | Число степе- ней свободы | Дисперсия | F – кри-терий |
| Между группами | 
| факторная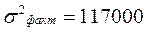 
| 
=56,83
| |
| Внутри групп |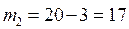 
| остаточная или случайная  
| ||
| Общая | 
| общая 
|
Табличное значение F –критерия: 
(приложение 2);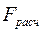 
> 
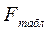поэтому зависимость между средней заработной платой и возрастом является существенной или статистически значимой.
2. Рассчитываем эмпирическое корреляционное отношение (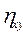
): 
.
где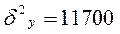 
; 
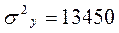(итоги решения прим. 6 в теме 5)
При подтверждении статистической зависимости для оценки тесноты связи рассчитываем коэффициент детерминации (
):
.
Зависимость между возрастом рабочих и средней месячной заработной платой очень тесная - на 87 % изменение зарплаты обусловлено возрастом рабочих.
Пример 2. По 12-ти предприятиям имеются следующие данные о годовой производительности труда работника (тыс.грн) и вооруженности труда основным капиталом (тыс.грн/чел.) (таблица 10.7).
На основании приведенных данных: 1) оцените тесноту связи между показателями с помощью коэффициента Фехнера и коэффициента ранговой корреляции Спирмена; 2) выявите зависимость и тесноту связи между показателями с помощью парного корреляционно-регрессионного анализа. Сделайте выводы.
Решение
1. Для определения коэффициента Фехнера рассчитываем средние значения признаков:
тыс.грн/чел, 
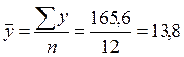тыс.грн.
Определяем знаки отклонений от среднего, т.е. знаки 
и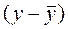 
и заносим в таблицу 10.6 (гр.3 и 4), а затем подсчитываем число совпадений и несовпадений знаков отклонений (гр.5). Тогда: 
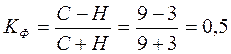. Коэффициент, равный 0,5 свидетельствует о наличии прямой и умеренной зависимости между производительностью труда и капиталовооруженностью труда.
Для определения коэффициента ранговой корреляции (
) проранжируем в порядке возрастания факторный и результативный признаки, т.е. определяем Rх и Rу и занесем их в гр.6 и 7 таблицы 10.7. Затем рассчитываем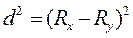 
и заносим в гр.8 данной таблицы. Тогда коэффициент ранговой корреляции Спирмена будет равен:
.
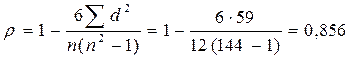Теснота связи между анализируемыми показателями прямая и достаточно тесная.
2. На первом этапе применения методики парного корреляционного анализа проверяем, выполняются ли требования, предъявляемые к факторному и результативному признакам.
- Однородность распределений. Все промежуточные расчеты представлены в таблице 10.8. 
; 
; 
; 
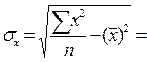
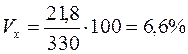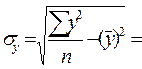
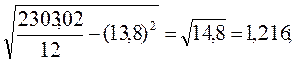
Коэффициенты вариации (
и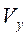 
) меньше 33%, что подтверждает гипотезу о статистической однородности и капиталовооруженности труда и производительности труда.
- Соответствие нормальному закону распределения.
По правилу “трех сигм” определяем интервалы:
а) для факторного признака 
; 
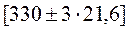или 
; хmin =298; хmax =366; отсюда 298 и 366 є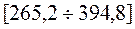 
, т.е. с вероятностью 0,997 можно утверждать, что факторный признак соответствует нормальному закону распределения;
б) для результативного признака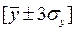 
; 
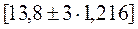или 
; уmin =12,5; уmax =16,3. Тогда:12,5 и 16,3 є .
Значит, с той же вероятностью и результативный признак соответствует нормальному закону распределения.
- Требования, связанные с независимостью по объектам наблюдения и взаимнооднозначном соответствии факторного и результативного признака, подтверждаются на этапе постановки задачи с помощью содержательного анализа исходной информации.
Следующая задача в методике парного корреляционно-регрес-сионного анализа – выбор формы связи между признаками. Для этого строим корреляционное поле (рис.10.1).
По расположению точек на корреляционном поле выбираем линейную форму связи, т.е. уравнение связи будет следующее: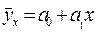 
.
Таблица 10.7
Расчетная таблица для определения непараметрических показателей тесноты связи
| № предприятия | Капиталовооруженность труда, тыс. грн/чел, х | Годовая производительность труда, тыс. грн., у | Знак отклонения от среднего | Число совпадений (несовпадений) знаков | Ранги |
 
| ||
факторного признака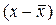 
| результативного признака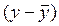 
| по х Rx | по у Rу | |||||
| 360,0 | 15,2 | + | + | С | ||||
| 298,0 | 12,8 | - | - | С | ||||
| 328,0 | 13,8 | - | Н | |||||
| 330,0 | 14,0 | + | С | |||||
| 366,0 | 16,3 | + | + | С | ||||
| 316,0 | 12,6 | - | - | С | ||||
| 334,0 | 13,2 | + | - | Н | ||||
| 300,0 | 12,9 | - | - | С | ||||
| 314,0 | 13,1 | - | - | С | ||||
| 320,0 | 12,5 | - | - | С | ||||
| 362,0 | 15,7 | + | + | С | ||||
| 332,0 | 13,5 | + | - | Н | ||||
| Всего | 3960,0 | 165,6 |
Таблица 10.8
Вспомогательные расчеты характеристик для парного корреляционно-регрессионного анализа
| № п/п | х | у | х2 | у2 | ху | 
| 
| 
| 
| 
|
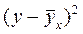
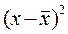
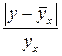
| 360,0 | 15,2 | 231,04 | 15,3 | 1,96 | 0,01 | 0,0066 | ||||
| 298,0 | 12,8 | 163,84 | 3814,4 | 12,2 | 1,0 | 0,36 | 0,047 | |||
| 328,0 | 13,8 | 190,44 | 4526,4 | 13,7 | 0,01 | 0,0072 | ||||
| 330,0 | 14,0 | 13,8 | 0,04 | 0,04 | 0,0143 | |||||
| 366,0 | 16,3 | 265,69 | 5965,8 | 15,6 | 6,25 | 0,49 | 0,043 | |||
| 316,0 | 12,6 | 158,76 | 3981,6 | 13,1 | 1,44 | 0,25 | 0,04 | |||
| 334,0 | 13,2 | 174,24 | 4408,8 | 14,0 | 0,36 | 0,64 | 0,134 | |||
| 300,0 | 12,9 | 166,41 | 12,3 | 0,81 | 0,36 | 0,0465 | ||||
| 314,0 | 13,1 | 171,61 | 4113,4 | 13,0 | 0,49 | 0,01 | 0,0076 | |||
| 320,0 | 12,5 | 156,25 | 13,3 | 1,69 | 0,64 | 0,064 | ||||
| 362,0 | 15,7 | 246,49 | 5683,4 | 15,4 | 3,61 | 0,09 | 0,019 | |||
| 332,0 | 13,5 | 182,25 | 13,5 | 0,09 | ||||||
| Всего | 3960,0 | 165,6 | 2303,02 | 54937,8 | 17,74 | 2,9 | 0,4292 |
 |
•
•
•
•
•
• •
•
•
• •
• •
 |
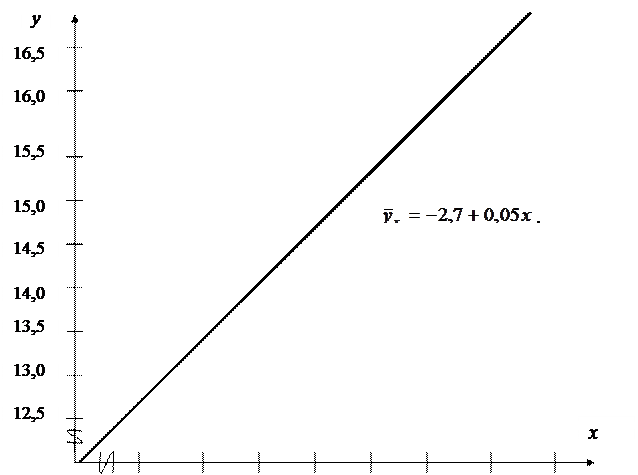……. - корреляционное поле;
- теоретическая линия регрессии.
Рис. 10.1. Корреляционное поле и теоретическая линия регрессии.
Определяем параметры а0 и а1 по упрощенным формулам, т.е.
.
где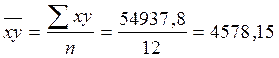 
; 
; 
;
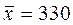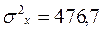Линейное уравнение связи будет иметь следующий вид: 
Параметр а1 = 0,05 показывает, что годовая производительность труда в среднем возрастет на 0,05 тыс.грн., если капиталовооруженность труда увеличится на одну тыс.грн., т.е. прирост капиталовооруженности на одну тыс. грн. сопровождается ростом производительности труда в среднем на 0,05 тыс.грн., а0 не имеет содержательной интерпретации.
Следующая задача – определение показателей тесноты связи. Рассчитываем:
- парный коэффициент корреляции: 
;
- парный коэффициент детерминации: 
;
коэффициент эластичности: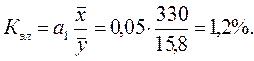 
Зависимость между капиталовооруженностью труда и годовой производительностью труда сложилась прямая (
) и достаточно тесная, в среднем на 83,0%, колеблемость (или изменение) производительности труда вызывается изменением капиталовооруженности труда. При этом каждый процент прироста капиталовооруженности труда сопровождается приростом производительности труда на 1,2%.
Следующая задача – проверка статистической значимости характеристик парного корреляционно-регрессионного анализа и статистической точности уравнения связи:
- парного коэффициента корреляции - на основе t -критерия (приложение 1):
; tтеор 
2,228; tрасч>tтабл.
С вероятностью 0,95 можно утверждать, что парный коэффициент корреляции статистически значимый или достоверный.
- уравнения связи - на основе F -критерия:
(расчет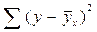 
и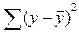 
представлен в гр.7 и 8 табл.10.8) 
, т.е. Fрасч > Fтабл (приложение 2).С вероятностью 0,95 можно утверждать, что линейное уравнение связи статистически достоверно.
- параметров уравнения связи - на основе t –критерия:
; 
; 
; 
; 
; 
; 
; 
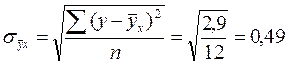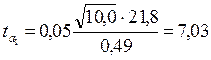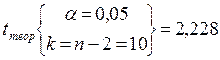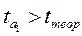, т.е. параметры уравнения связи являются статистически достоверными или надежными. Для проверки статистической точности уравнения связи рассчитываем относительную ошибку аппроксимации (гр.10, табл.10.8)
, 
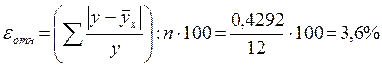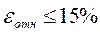, что подтверждает статистическую точность полученного уравнения регрессии.
Пример 3. Известны следующие данные о валовом доходе и оборотных средствах торгового предприятия по кварталам 2001 и 2002гг.
| Кварталы | Стоимость оборотных средств, тыс.грн. | Валовой доход, тыс.грн. |
| 2001 год | ||
| 50,0 | 63,0 | |
| П | 56,0 | 70,0 |
| Ш | 35,0 | 48,0 |
| 1V | 36,0 | 50,0 |
| 2002 год | ||
| 40,0 | 60,0 | |
| П | 45,0 | 54,0 |
| Ш | 42,0 | 70,0 |
| 1V | 48,0 | 65,0 |
Выявите зависимость между валовым доходом и стоимостью оборотных средств с помощью методики корреляционно-регрессион-ного анализа. Обоснуйте выбор размерности уравнения связи и способа его расчета. Сделайте выводы.
Решение
1. По условию представлены ряды динамики, уровни которых автокоррелированы по своему содержанию, так как стоимость оборотных средств в каждом квартале частично включает их стоимость за предыдущий период. Аналогичная зависимость характерна и для валового дохода. Поэтому уравнение регрессии строим по способу включения фактора времени в качестве независимой переменной, т.е.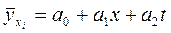 
.
Тогда система нормальных уравнений будет следующей:
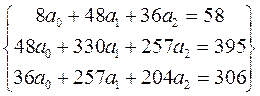
Все промежуточные расчеты представлены в таблице 10.9. В результате решения получаем такие значения параметров:
; 
; 
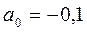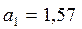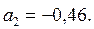
Множественное уравнение регрессии будет иметь следующий вид: 
.
Подставив в уравнение регрессии соответствующие х и t для каждого периода наблюдения, определяем расчетное значение результативного признака (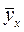
), т.е. валового дохода (гр.10 табл. 10.9).
Параметр а1 = 1,57 показывает, что увеличение стоимости оборотных средств на один млн.грн. сопровождается приростом валового дохода в среднем на 1,57 млн.грн. при условии, что фактор времени не варьирует, т.е. зафиксирован на уровне своего среднего значения. Параметр а2 при факторе времени не имеет содержательной интерпретации.
Для оценки тесноты связи рассчитаем множественный коэффициент корреляции и детерминации. При учете влияния двух факторов (х и t) можно использовать следующую формулу:
,
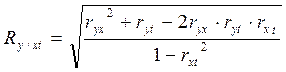где 
- парные коэффициенты корреляции между соответствующими факторами.
; 
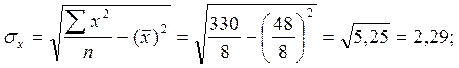
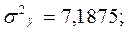
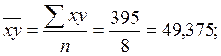
По аналогии определяем:
;
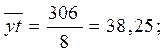
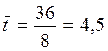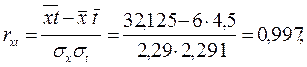
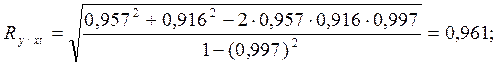
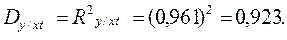
Зависимость между валовыми доходами предприятия, стоимостью оборотных средств и фактором времени достаточно тесная, - на 92,3% изменение валового дохода обусловлено влиянием данных факторов.
Для проверки статистической достоверности уравнения связи рассчитываем F –критерий: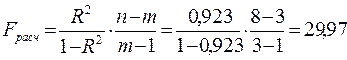 
;
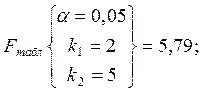F расч > F табл, что подтверждает статистическую достоверность полученного уравнения связи.
Пример 4. Распределение ответов респондентов, проживающих в городской и сельской местности, по оценке своего уровня материальной обеспеченности было следующим:
| Место проживания | Уровень материальной обеспеченности | |
| обеспеченный | необеспеченный | |
| Город | 17,6 (а) | 84,2 (в) |
| Село | 15,5 (с) | 84,1 (d) |
Определите, существует ли зависимость между местом проживания и оценкой своего уровня материальной обеспеченности.
Решение
1. Рассчитываем коэффициент ассоциации: 
Таблица 10.9
Вспомогательная таблица для расчета параметров уравнения связи
| № пп | Стоимость оборотных средств, млн. грн. | Валовой доход, млн.грн | Время, t | х2 | у2 | t 2 | ху | t у | t х | 
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| 4,15 | ||||||||||
| 5,26 | ||||||||||
| 4,8 | ||||||||||
| 5,91 | ||||||||||
| 7,02 | ||||||||||
| 9,7 | ||||||||||
| 9,24 | ||||||||||
| 11,92 | ||||||||||
| Итого |
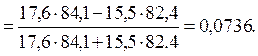Зависимости практически нет, т.е. не-зависимо от места проживания населения одинаково оценивает уровень метариальной обеспеченности.
2. Определяем коэффициент контингенции:
= 
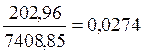. Значение коэффициента контингенции подтверждает вывод о несущественной зависимости между местом проживания и оценкой своего уровня материальной обеспеченности.
Пример 5. Для изучения влияния условий производства на взаимоотношения в коллективе было проведено обследование 300 работающих, ответы которых распределились следующим образом.
| Условия производства | Взаимоотношения в коллективе | |||
| xоро- шие | удовлетво- рительные | неудовлетво-рительные | итого | |
| Соответствуют требованиям | ||||
| Не полностью соответствуют | ||||
| Не соответствуют | ||||
| Итого |
Определите зависимость между условиями производства и взаимоотношениями в коллективе с помощью коэффициентов взаимной сопряженности К. Пирсона и А. Чупрова. Сделайте выводы.
Решение
Коэффициент взаимной сопряженности К.Пирсона рассчитывается по формуле: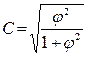 
; 
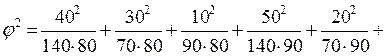
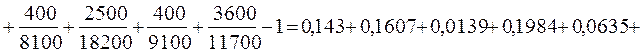
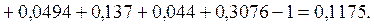
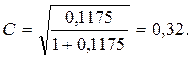
Коэффициент взаимной сопряженности А.Чупрова определяется по соотношению: 
.
Полученные значения коэффициентов (< 0,5) свидетельствуют, что связь между условиями производства и взаимоотношениями в коллективе несущественная, т.е. взаимоотношения в коллективе не связаны с условиями производства.
Пример 6. Заданы следующие показатели по 16 металлургическим предприятиям:
| № пп | Производительность труда, тыс. грн. на одного занятого, x | Фондоотдача, грн., z | Рентабельность продукции, %, у |
| 1 | 2 | 3 | 4 |
| 29,4 | 0,36 | - 28,4 | |
| 37,6 | 1,6 | - 9,0 | |
| 86,7 | 1,41 | 5,62 | |
| 79,6 | 1,4 | 5,76 | |
| 5,1 | 1,3 | - 5,58 | |
| 41,1 | 1,62 | -18,9 | |
| 20,9 | 0,6 | - 40,8 | |
| 34,8 | 0,7 | -13,8 | |
| 56,0 | 1,0 | - 3,6 | |
| 47,0 | 0,8 | -15,8 | |
| 88,2 | 1,31 | 11,4 | |
| 56,2 | 0,9 | - 2,3 | |
| 51,9 | 1,15 | - 2,2 | |
| 38,0 | 3,1 | 2,60 | |
| 7,7 | 0,24 | 2,1 | |
| 36,9 | 0,89 | - 2,22 |
Определите: 1) коэффициент конкордации; 2) проверьте статистическую достоверность полученного коэффициента. Сделайте выводы.
Решение
Определяем ранги сопоставляемых показателей (табл.10.10).
;.
Между производительностью труда, фондоотдачей и уровнем рентабельности продукции сложилась достаточно тесная зависимость.
Для проверки значимости коэффициента координации рассчитывается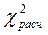 
: 
.
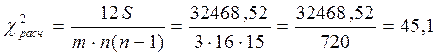По таблицам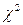 
-распределения (приложение 4) при 
и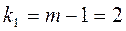 
, 
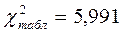, соотношение 
> 
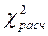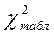свидетельствует о статистической достоверности коэффициента конкордации.
Таблица 10.10
Расчет коэффициента конкордации
| № п/п | 
| 
| 
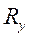
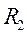
| Сумма рангов по строке ( )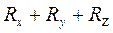
| Квадраты суммы строк
( )2
|
| Итого |
