ВзаимОСВЯЗЕЙ социально-экономических
Явлений
Методические указания
Статистические зависимости между переменными по своему содержанию бывают двух видов: функциональные и стохастические или вероятностные, - частным случаем стохастической связи выступает корреляционная.
Функциональные зависимости изучаются с помощью индексного анализа и балансового метода. При стохастических зависимостях применяются следующие методы изучения связей:
- метод аналитических группировок;
- дисперсионный анализ;
- корреляционно-регрессионный анализ;
- непараметрические методы или методы сравнения параллельных рядов;
- методы оценки взаимосвязей между альтернативными и атрибутивными признаками.
Метод аналитических группировок. По итогам аналитической группировки1 устанавливается наличие (или отсутствие) зависимости между факторным, т.е. группировочным (х) и результативным (у) признаками и ее направление на основе сопоставления характера изменения средних значений результативного признака ( ) и изменения среднего значения факторного признака (
) и изменения среднего значения факторного признака (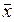 і).
і).
Дополнительно можно рассчитать количественные характеристики меры изменения результативного признака при изменении факторного на определенную величину, которые называются показателями силы связи: 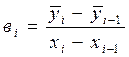 или
или  .
.
где  ,
, 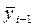 - среднее значение результативного признака по i -ой и (i -1)-ой группах; i =
- среднее значение результативного признака по i -ой и (i -1)-ой группах; i =  ; k - число групп;
; k - число групп;  ,
,  - дискретные значения факторного признака по i -ой и (i -1)-ой группах;
- дискретные значения факторного признака по i -ой и (i -1)-ой группах;  ,
, 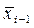 - средние значения факторного признака соответствующих групп.
- средние значения факторного признака соответствующих групп.
Показатели вi рассчитываются для каждой группы и различия в их значении по отдельным группам показывают, в какой мере изменение результативного признака зависит от значения факторного.
В случае линейной связи рассчитывается показатель средней силы связи:  или
или 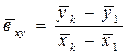
где  ,
,  - среднее значение результативного признака в последней и первой группе, соответственно;
- среднее значение результативного признака в последней и первой группе, соответственно;  ,
, 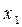 - дискретные значения факторного признака в соответствующих группах;
- дискретные значения факторного признака в соответствующих группах; 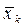 ,
,  - средние значения факторного признака по этим же группам.
- средние значения факторного признака по этим же группам.
В случае прямой связи 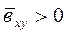 , обратной -
, обратной -  . Для нелинейных связей показатель средней силы связи не имеет значения.
. Для нелинейных связей показатель средней силы связи не имеет значения.
Дисперсионный анализ дает возможность определить роль систематической и случайной вариации в общей вариации признака. Для этого общая вариация подразделяется на указанные составляющие и производится сравнение этих составляющих. Чаще всего эта задача решается совместно с аналитической группировкой (глава 2). В этом случае вся изучаемая совокупность делится на группы по факторному признаку, а затем вычисляются значения средних величин по результативному признаку в каждой группе  . Необходимо определить, существенно ли различие между средними значениями результативного признака в группах, которое как раз и обусловлено влиянием факторного признака.
. Необходимо определить, существенно ли различие между средними значениями результативного признака в группах, которое как раз и обусловлено влиянием факторного признака.
Если число выделенных групп всего две, то для проверки данной гипотезы применяется t – критерий, а если больше двух, то используется F – критерий.
Рассмотрим случай группировки по одному признаку, т.е. однофакторный дисперсионный комплекс. В качестве меры вариации в дисперсионном анализе используется не дисперсия, а девиация, т.е. сумма квадратов отклонений признака от средней:  Поэтому вместо правила разложения дисперсий используется аналогичное правило разложения девиаций, т.е:
Поэтому вместо правила разложения дисперсий используется аналогичное правило разложения девиаций, т.е:

где уij – значение результативного признака j -ой единицы совокупности в і- ой группе; j - номер единицы совокупности,  ; i – номер группы;
; i – номер группы; 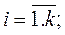 k - число групп; fi - размер i -той группы или число единиц в i -той группе;
k - число групп; fi - размер i -той группы или число единиц в i -той группе; 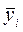 - среднее значение результативного признака в і- той группе;
- среднее значение результативного признака в і- той группе;  ;
;  - общая средняя результативного признака.
- общая средняя результативного признака.
Если обозначить суммы квадратов отклонений буквой Д, то получим следующее равенство:  . На основе данного соотношения рассчитываются три оценки дисперсии пропорционально соответствующим числам степеней свободы; при этом число степеней свободы равно:
. На основе данного соотношения рассчитываются три оценки дисперсии пропорционально соответствующим числам степеней свободы; при этом число степеней свободы равно:
- для общей вариации:  ;
;
- для межгрупповой вариации:  ;
;
- для остаточной вариации: 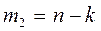 .
.
Числа степеней свободы связаны между собой равенством, аналогичному взаимосвязи дисперсий и девиации, т.е.  ;
; 
Деление девиации на соответствующее число степеней свободы дает три оценки дисперсии:
- общая дисперсия:  ;
;
- межгрупповая (или факторная) дисперсия:  ;
;
- остаточная или случайная дисперсия: 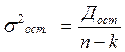 .
.
Д факт и, соответственно, межгрупповая дисперсия измеряет вариацию результативного признака, связанную с изменением факторного, Д ост – вариацию, связанную с изменением всех остальных факторов. Соотношение девиаций, рассчитанных на одну степень свобо-ды, дает возможность оценить существенность влияния факторного признака на результативный с помощью F – критерия:
 , при этом
, при этом 
По таблицам F -распределения (приложение 2) с заданным уровнем статистической достоверности α и по числу степеней свободы m1 и m2, находим Fтабл, и, если Fрасч > Fтабл, можно утверждать, что влияние факторного признака на изменение результативного является существенным или статистически значимым. Схема однофакторного дисперсионного анализа представлена в таблице 10.1.
Таблица 10.1






