Ø относительное изменение средней цены отдельного товара; 2) аб-солютное изменение средней цены в отчетном периоде по сравне-нию с базисным; 3) абсолютное изменение средней цены отдель-ного товара за счет изменения структуры продажи; 4) индекс структурных сдвигов.
Что можно установить по формуле:?
Ø относительное изменение средней цены товара; 2) динамику средней по группе объектов цены товара за счет изменения её индивидуальных уровней по каждому объекту; 3) относи-тельное изменение цен по нескольким товарам; 4) динамику средней по группе объектов цены товара за счет изменения структуры проданных товаров.
17. Какая из приведенных формул является индексом средней
себестоимости переменного состава:
1) 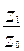 ; 2)
; 2) 
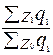 ; 3)
; 3) 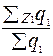 :
: 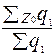 ; 4)
; 4) 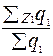 :
: 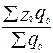 ?
?
18. По какой из приведенных формул нельзя рассчитать индекс цен постоянного состава:
1) 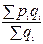 :
: 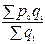 ; 2)
; 2)  ; 3)
; 3) 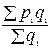 :
: 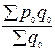 ; 4)
; 4)  ?
?
Решение типовых задач
Пример 1. Имеются следующие данные о производстве про-дукции на заводе:
| Вид из-делия | Объем производства, тыс.шт | Себестоимость, тыс.грн./шт | ||
| базисный период | отчетный период | базисный период | отчетный период | |
| А | 2,5 | 3,0 | ||
| Б | 1,4 | 1,75 |
Вычислите: 1) индивидуальные индексы себестоимости, физи-ческого объема производства и затрат на производство продукции А; 2) общий индекс затрат; 3) общий индекс физического объема про-изводства продукции; 4) общий индекс себестоимости; 5) общее аб-солютное изменение затрат на производство продукции, в том числе за счет изменения количества и себестоимости продукции. Покажите взаимосвязь между исчисленными индексами.
Решение
2. Индивидуальные индексы рассчитаем для изделия “А”:
а) себестоимости  ;
; 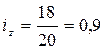 или 90%, т.е. себестоимость изделия А снизилась на 10%.
или 90%, т.е. себестоимость изделия А снизилась на 10%.
б) количества произведенной продукции:  ;
;  или 120%, т.е. объем производства этого изделия вырос на 20%.
или 120%, т.е. объем производства этого изделия вырос на 20%.
в) затрат на производство продукции: 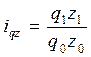 ;
; 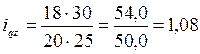 или 108%, т.е. затраты на производство продукции А выросли на 8%.
или 108%, т.е. затраты на производство продукции А выросли на 8%.
3. Общий (агрегатный) индекс затрат определяется по формуле:
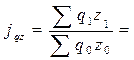
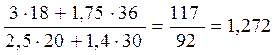 или 127,2 %, т.е. затраты на производство в отчетном периоде по сравнению с базисным увеличились на 27,2 %.
или 127,2 %, т.е. затраты на производство в отчетном периоде по сравнению с базисным увеличились на 27,2 %.
4. Общий (агрегатный) индекс физического объема производст-ва продукции равен: 
 или 122,3 % т.е. общий объем производства продукции вырос на 22,3 %.
или 122,3 % т.е. общий объем производства продукции вырос на 22,3 %.
5. Общий (агрегатный) индекс себестоимости равен:

 или 104 %, т.е. себестои-мость всей разнородной продукции выросла в среднем на 4 %.
или 104 %, т.е. себестои-мость всей разнородной продукции выросла в среднем на 4 %.
5. Общее абсолютное изменение затрат на производство продук-ции в отчетном периоде по сравнению с базисным определяется по данным общего индекса затрат и равно разности между числителем и знаменателем этого индекса: 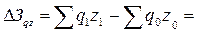 117-92=25 тыс.грн.
117-92=25 тыс.грн.
Абсолютное изменение затрат на производство продукции за счет изменения объема производства определяется по данным общего индекса физического объема производства и равно разности между числителем и знаменателем этого индекса: 
= 112,5 – 92 = 20,5 тыс. грн.
Абсолютное изменение затрат на производство продукции за счет изменения себестоимости изделий определяется по данным общего индекса себестоимости и равно разности между числителем и знаменателем этого индекса: 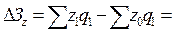 117-112,5=4,5 тыс.грн.
117-112,5=4,5 тыс.грн.
Таким образом, в отчетном периоде по сравнению с базисным затраты на производство продукции выросли на 27,2 % или на 25 тыс. грн. Объем производства продукции вырос на 22,3 % и за счет этого затраты на производство продукции выросли на 20,5 тыс.грн. Себес-тоимость продукции выросла на 4 %, и это привело к увеличению затрат на 4,5 млн.грн. Между исчисленными индексами существует взаимосвязь 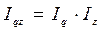 =1,223 · 1,040 = 1,272.
=1,223 · 1,040 = 1,272.
Пример 2. По имеющимся данным о производстве продукции на заводе вычислите: 1) общий индекс физического объема произ-водства продукции; 2) как изменилась стоимость произведенной про-дукции под влиянием изменения количества произведенных изделий.
| Вид изделия | Произведено в прошлом году, тыс.грн. | Индекс количества произведенной продукции в текущем году по сравнению с прошлым годом |
| Пылесосы Электроутюги | 0,95 1,20 | |
| Итого | - |
Решение
1. Для определения относительного изменения объема произ-водства продукции в текущем году по сравнению с прошлым годом следует использовать средний арифметический индекс:
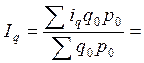
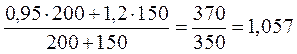 или 105,7 %
или 105,7 %
Следовательно, объем производства двух видов продукции по заводу вырос на 5,7 %.
2. 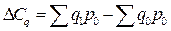 =370-350 = +20 тыс. грн.; т.е. рост физичес-кого объема производства привел к увеличению стоимости произве-денной продукции в текущем году на 20 тыс.грн.
=370-350 = +20 тыс. грн.; т.е. рост физичес-кого объема производства привел к увеличению стоимости произве-денной продукции в текущем году на 20 тыс.грн.
Пример 3. Имеются следующие данные о продаже товаров по центральному универмагу города:
| Товарные группы | Товарооборот ΙΙ квартала, тыс.грн | Увеличение (+), уменьшение (-) цены во ΙΙ квартале по сравнению с I кварталом, % |
| Ткани | 61,5 | +105 |
| Галантерея | 16,5 | -3 |
Вычислите: 1) общий индекс цен; 2) сумму экономии или пер-расхода, вызванную изменением цен.
Решение
2) Общий индекс цен равен: 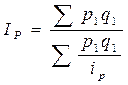 . Для вычисления этого индекса определим предварительно индивидуальные индексы цен:
. Для вычисления этого индекса определим предварительно индивидуальные индексы цен:
для тканей: iР = 100 + 105 = 205% или 2,05;
для галантереи: iР = 100 – 3 = 97% или 0,97.
Тогда: 
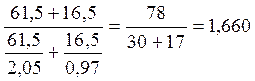 или 166%, т.е. цены на товары во ΙΙ квартале по сравнению с Ι кварталом выросли на 66%.
или 166%, т.е. цены на товары во ΙΙ квартале по сравнению с Ι кварталом выросли на 66%.
3) Перерасход, вызванный изменением цен, составил:
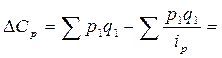 78 – 47 = 31 тыс.грн.
78 – 47 = 31 тыс.грн.
Пример 4. Имеются следующие данные о продаже товаров в универсаме № 1:
| Товары | Товарооборот в дейст-вующих ценах, тыс.грн. | Изменение цен во ΙΙ квартале по сравнению с I,% | |
| I квартал | ΙΙ квартал | ||
| Колбасные изделия | +25 | ||
| Рыба и рыбные продукты | -7 |
Вычислите: 1) общий индекс товарооборота, 2) общий индекс цен; 3) общий индекс физического объема товарооборота; 4) эконо-мию или дополнительные расходы населения, вызванные изменением цен.
Решение
2) Общий индекс товарооборота равен: 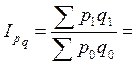
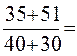 = 1,229 или 122,9%, т.е. товарооборот во ΙΙ квартале по сравнению с I кварталом возрос на 22,9% или на 16 тыс.грн. (86 – 70).
= 1,229 или 122,9%, т.е. товарооборот во ΙΙ квартале по сравнению с I кварталом возрос на 22,9% или на 16 тыс.грн. (86 – 70).
3) Общий индекс цен определяем по формуле:  .
.
Индивидуальные индексы цен равны:
по колбасным изделиям: iР = 100 + 25 = 125 %,
по рыбе и рыбным продуктам: iР = 100 – 7 = 93 %.
Тогда  или 103,8%, т.е. цены на то-вары выросли на 3,8%, что привело к росту товарооборота на 3,16 тыс.грн. (86 - 82,84).
или 103,8%, т.е. цены на то-вары выросли на 3,8%, что привело к росту товарооборота на 3,16 тыс.грн. (86 - 82,84).
3. Общий индекс физического объема товарооборота определим исходя из взаимосвязи индексов:  =1,229: 1,038 = 1,184 или 118,4%, т.е. физический объем продажи товаров вырос на 18,4%.
=1,229: 1,038 = 1,184 или 118,4%, т.е. физический объем продажи товаров вырос на 18,4%.
4. Дополнительные расходы населения, вызванные ростом цен на товары составили: 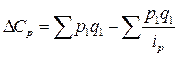 = 86,0 - 82,84 = 3,16 тыс.грн., т.е. они равны исчисленному выше приросту товарооборота за счет роста цен.
= 86,0 - 82,84 = 3,16 тыс.грн., т.е. они равны исчисленному выше приросту товарооборота за счет роста цен.
Пример 5. Имеются следующие данные о продаже картофеля на двух рынках города:
| Номер рынка | Базисный период | Отчетный период | ||
| продано,тыс.кг | цена за 1кг,грн | продано,тыс.кг | цена за 1кг,грн | |
| 1,30 | 1,35 | |||
| 1,40 | 1,32 |
Вычислите: 1) индекс средней цены переменного состава; 2) ин-декс средней цены постоянного состава; 3) индекс средней цены структурных сдвигов; 4) абсолютное изменение средней цены картофеля всего, в том числе за счет изменения: а) цены на каждом рынке; б) структуры продажи картофеля; 5) абсолютное изменение товарооборота, вызванное изменением объема, структуры продажи и цен на картофель.
Решение
3) Индекс цены переменного состава равен: 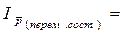
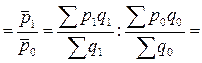
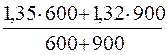 :
: 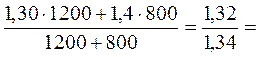
= 0,985 или 98,5%. Средняя цена картофеля в отчетном периоде по сравнению с базисным снизилась на 1,5%. Это снижение вызвано изменением цены картофеля и структуры его продажи по рынкам.
4) Индекс цены постоянного состава равен: 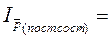
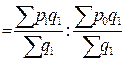
 0,971 или 9,71%. Средняя цена картофеля за счет изменения цен на рынке снизилась на 2,9%.
0,971 или 9,71%. Средняя цена картофеля за счет изменения цен на рынке снизилась на 2,9%.
5) Индекс цены структурных сдвигов: 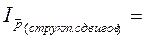

 1,015 или 101,5%, т.е. изменение структуры продажи картофеля по рынкам привело к росту средней цены картофеля на 1,5%.
1,015 или 101,5%, т.е. изменение структуры продажи картофеля по рынкам привело к росту средней цены картофеля на 1,5%.
6) В отчетном периоде по сравнению с базисным средняя цена картофеля снизилась на: 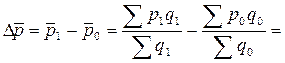 1,32 – 1,34 = = - 0,02 грн., в том числе за счет изменения:
1,32 – 1,34 = = - 0,02 грн., в том числе за счет изменения:
а) цены на картофель по рынкам: 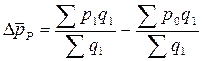 = 1,32 – 1,36 =
= 1,32 – 1,36 =
= - 0,04 грн.;
б) структуры продажи картофеля:  = 1,36 – 1,34 = = 0,02 грн.
= 1,36 – 1,34 = = 0,02 грн.
7) Абсолютное изменение товарооборота определяется так:
а) за счет изменения объема продажи картофеля:
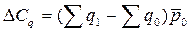 = (1500-2000) · 1,34 = - 670 тыс.грн;
= (1500-2000) · 1,34 = - 670 тыс.грн;
б) за счет изменения структуры продажи картофеля:
 = 2040 - 1,34 · 1500 = 30 тыс.грн. или
= 2040 - 1,34 · 1500 = 30 тыс.грн. или
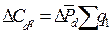 = + 0,02 · 1500 = 30 тыс.грн;
= + 0,02 · 1500 = 30 тыс.грн;
в) за счет изменения цены картофеля по рынкам:
 = 1980 – 2040 = - 60 тыс.грн. или
= 1980 – 2040 = - 60 тыс.грн. или
 = - 0,04 · 1500 = - 60 тыс.грн.
= - 0,04 · 1500 = - 60 тыс.грн.
Таким образом, 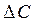 =
= 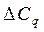 +
+ 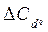 +
+ 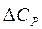 = -670 + 30 + (-60) =
= -670 + 30 + (-60) =
= -700тыс.грн.
Пример 6. По имеющимся данным о работе предприятия за два сравниваемых периода установите абсолютное изменение производительности труда в целом и, в т.ч., за счет: а) среднечасовой производительности труда (Wчас .); б) средней фактической продолжительности рабочего дня (tч); в) средней фактической продолжительности рабочего периода (tд), доли рабочих в общем числе работающих на предприятии (dp):
| № пп | Наименование показателя | Усл.обоз начения | Период | Темп роста,% | |
| базисный | отчетный | ||||
| Объем произведенной продукции, тыс.грн. | q | 1460,25 | 1837,57 | 125,84 | |
| Среднесписочная численность работающих, чел. | Т | 115,40 | |||
| Среднесписочная численность рабочих-сдельщиков, чел. | Тр | 120,00 | |||
| Общее число отработанных рабочими-сдельщиками:а) человеко-дней,тыс | Тч-д | 88,50 | 102,50 | 115,93 | |
| б) человеко-часов, тыс. | Тч-ч | 663,70 | 759,24 | 114,38 | |
| Среднечасовая выработка - ([1]: [4-б]), грн. | Wчас | 2,20 | 2,42 | 110,00 | |
| Средняя дневная выработка-([1]:[4-а]), грн. | Wдн. | 16,50 | 17,93 | 108,67 | |
| Средняя производительность труда 1-го рабочего ([1]:[3]),грн | Wр | 973,50 | 1020,87 | 104,87 | |
| Средняя производительность труда 1-го работающего, грн. | W | 486,75 | 530,78 | 109,05 | |
| Средняя продолжительность: а) рабочего периода ([4а]: [3]) | tд | 59,00 | 56,94 | 96,51 | |
| б) рабочего дня ([4б]: [4а]),грн. | tч | 7,50 | 7,41 | 98,80 | |
| Доля рабочих в общем числе работающих ([3]: [2] 100), % | dp | 50,0 | 51,99 | 103,99 |
Решение
Решить поставленную задачу можно путем построения взаимосвязанных частных индексов с последующим нахождением разности числителя и знаменателя каждого индекса. Проведем расчеты, используя: 1) две схемы разложения: а) обособленного учета влияния показателей-факторов; б) цепной схемы; 2) прием цепных показателей.
Покажем достоинства и недостатки каждого способа.
Взаимосвязь исследуемого сложного экономического показателя (средней выработке на одного работающего - w) и показателей – факторов можно выразить мультипликативной моделью, которая в зависимости от желаемой степени детализации анализа может принимать одну из следующих форм: w = wчас· tч· tд· dр= wдн· tд· dр= wр · dр.
Абсолютный прирост средней производительности труда 1-го работающего составит: Δ w = 530,78 – 486,75 + 44,03 грн.
Данный прирост формировался под влиянием разнонаправленного изменения показателей - факторов. Оценим роль каждого фактора по схеме обособленного учета их влияния:
а) влияние среднечасовой производительности труда (wr):
- относительное: 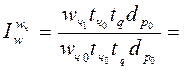
 = 1,10 или 110%, т.е. рост среднечасовой выработки на 10% привел к та-кому же относительному увеличению результативного показателя (показателя – функции – w);
= 1,10 или 110%, т.е. рост среднечасовой выработки на 10% привел к та-кому же относительному увеличению результативного показателя (показателя – функции – w);
- абсолютное:  = 535,42 – 486,75 = + 48,68 грн;
= 535,42 – 486,75 = + 48,68 грн;
б) влияние средней фактической продолжительности рабочего дня (tч):
относительное: 
 = 0,988 или 98,8%, т.е. средняя выработка на 1-го работающего снизилась на 1,2% вследствие сокращения средней фактической продолжитель-ности рабочего дня:
= 0,988 или 98,8%, т.е. средняя выработка на 1-го работающего снизилась на 1,2% вследствие сокращения средней фактической продолжитель-ности рабочего дня:
- абсолютное: 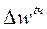 = 480,91 – 486,75 = - 5,84 грн
= 480,91 – 486,75 = - 5,84 грн
в) влияние средней фактической продолжительности рабочего пе-риода (tд):
- относительное: 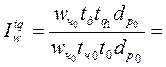
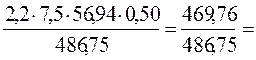 0,965 или 96,5%, т.е. сокращение средней фактической продолжительнос-ти рабочего периода привело к сокращению выработки на 1-го ра-ботающего на 3,5%.
0,965 или 96,5%, т.е. сокращение средней фактической продолжительнос-ти рабочего периода привело к сокращению выработки на 1-го ра-ботающего на 3,5%.
- абсолютное: 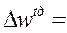 469,76 - 486,75 = -16,99 грн.;
469,76 - 486,75 = -16,99 грн.;
г) влияние доли рабочих (dp):
- относительное: 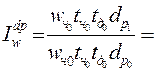
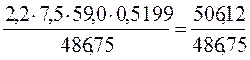 = 1,0399 или 103,99%, т.е. выработка на 1-го работающего выросла почти на 4% за счет роста доли рабочих в общей численности персонала;
= 1,0399 или 103,99%, т.е. выработка на 1-го работающего выросла почти на 4% за счет роста доли рабочих в общей численности персонала;
- абсолютное: 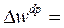 506,12 – 486,75 = +19,37 грн.
506,12 – 486,75 = +19,37 грн.
Достоинством рассмотренной схемы разложения общего прирос-та является то, что очередность рассмотрения влияния показателей-факторов не играет никакой роли. Те же результаты были бы получе-ны при любой другой последовательности, т.к. всякий раз изменяется только учитываемый показатель-фактор, а все прочие (уже рассмот-ренные ранее и те, учет влияния которых еще предстоит провести) берутся на базисном уровне (предполагается, что они не менялись и не влияли на динамику результативного показателя).
Кроме названного достоинства следует акцентировать внимание на существенном недостатке этого метода, а именно: он не дает пол-ного разложения, т.е. произведение частных индексов не дает индекса результативного показателя, а сумма частных приростов не совпадает с общим абсолютным приростом.
 1,0399 · 0,9651 · 0,988 · 1,100 ≠ 1,0905.
1,0399 · 0,9651 · 0,988 · 1,100 ≠ 1,0905.
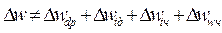 =19,37 +(-16,91) +(-5,84) + 48,68 ≠ 44,03 грн.
=19,37 +(-16,91) +(-5,84) + 48,68 ≠ 44,03 грн.

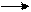
 Применяя для анализа динамики показателя производительности труда 1-го работающего цепную схему разложения можно устранить указанный недостаток и получить полное разложение. Однако следует особо оговаривать очередность рассмотрения показателей-факторов. Чтобы следовать общепринятому правилу построения агрегатной формы индексов (рассмотрено выше) примем очередность: dp tд tч wч. При цепной схеме разложения на каждом следующем шаге расчетов уже рассмотренный ранее фактор будет приниматься на уровне отчетного периода и в числителе, и в знаменателе частного индекса:
Применяя для анализа динамики показателя производительности труда 1-го работающего цепную схему разложения можно устранить указанный недостаток и получить полное разложение. Однако следует особо оговаривать очередность рассмотрения показателей-факторов. Чтобы следовать общепринятому правилу построения агрегатной формы индексов (рассмотрено выше) примем очередность: dp tд tч wч. При цепной схеме разложения на каждом следующем шаге расчетов уже рассмотренный ранее фактор будет приниматься на уровне отчетного периода и в числителе, и в знаменателе частного индекса:
а) влияние доли рабочих (dp):
- относительное: 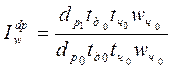
 = 1,0399 или 103,99 %
= 1,0399 или 103,99 %
абсолютное:  506,12 – 486,75 = + 19,37 грн.;
506,12 – 486,75 = + 19,37 грн.;
б) влияние средней фактической продолжительности рабочего пе-риода (tд):
- относительное: 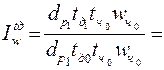
 = 0,9651 или 96,51%
= 0,9651 или 96,51%
- абсолютное: 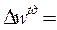 488,45 – 506,12 = - 17,67 грн;
488,45 – 506,12 = - 17,67 грн;
в) влияние средней фактической продолжительности рабочего дня (tч):
относительное: 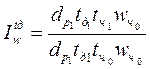
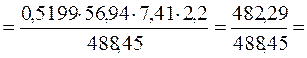
= 0,9889 или 98,8 %;
абсолютное: 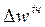 = 482,29 – 488,45 = - 616 грн;
= 482,29 – 488,45 = - 616 грн;
г) влияние среднечасовой производительности труда (wч):
- относительное: 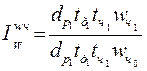 =
= 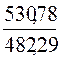 = 1,101 или 110,1%
= 1,101 или 110,1%
абсолютное:  = 530,78 – 482,29 = 48,49 грн.
= 530,78 – 482,29 = 48,49 грн.
Суммарное влияние составит:19,37 +(-17,67) +(-6,16) +48,49= 44,03.
Таким образом, мы получили полное разложение:
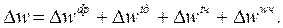
Прием цепных показателей дает, с одной стороны, полное разложение, а с другой – не требует оговаривания последовательности рассмотрения показателей факторов (другими словами, он устраняет недостатки каждой из рассмотренных схем разложения).
Построение цепного показателя – фактора осуществляется так: в числителе берется разность индексов числителя и знаменателя рас-четной формулы показателя-фактора, а в знаменателе – всегда индекс знаменателя показателя-функции в нашем случае - (w). Полученная дробь, указывающая на относительное изменение сложного явления за счет рассматриваемого фактора, умножается на уровень показателя функции базисного периода в нашем случае - (w о). Этим умножением достигается получение абсолютной величины того же изменения.
Таким образом, если помнить, что 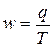 , то влияние отдельных показателей-факторов на изменения этого сложного явления будет установлено так:
, то влияние отдельных показателей-факторов на изменения этого сложного явления будет установлено так:
а) влияние доли рабочих ( ):
): 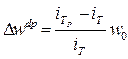
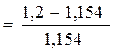 486,75 = = +19,40 грн.;
486,75 = = +19,40 грн.;
б) влияние средне фактической продолжительности рабочего перио-да (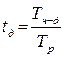 ):
): 
 486,75 = - 17,17 грн.;
486,75 = - 17,17 грн.;
в) влияние средней фактической продолжительности рабочего дня:
(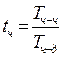 ):
): 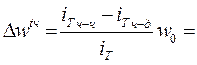
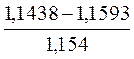 486,75 = - 6,54 грн.;
486,75 = - 6,54 грн.;
г) влияние среднечасовой производительности труда (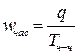 ):
):

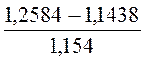 486,75 = + 48,54 грн.
486,75 = + 48,54 грн.
 19,40 +(-17,17)+ (-6,54) + 48,34 = 44,03грн.
19,40 +(-17,17)+ (-6,54) + 48,34 = 44,03грн.






