| Источник вариации | Сумма квадра-тов отклонений (девиация) | Число степеней свободы | Средний квадрат отклонений, вид дисперсии | F – крите рий |
| Между группами | 
|
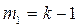
| факторная
|
|
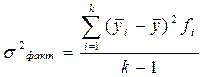
| Внутри групп | 
|
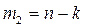
| остаточная или случайная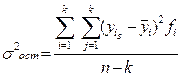  
| |
| Общая | 
|
| общая 
|
После подтверждения гипотезы о статистической существенности влияния факторного признака на изменение результативного рассчитываются показатели тесноты связи между ними.
По итогам аналитической группировки по результативному признаку рассчитываются три вида дисперсий – общая (
), межгрупповая (
)и внутригрупповая, т.е. средняя из групповых (
)2. Их соотношения позволяют рассчитать два показателя тесноты связи между факторным и результативным признаками:
- эмпирическое корреляционное отношение: 
;
- коэффициент детерминации: 
.
Эмпирическое корреляционное отношение характеризует тесноту связи между изучаемыми факторами, а коэффициент детерминации измеряет, какая часть общей колеблемости результативного признака вызывается колеблемостью факторного. Они принимают значения в интервале [0,1]: чем ближе к 1, тем теснее связь, и, наоборот. По шкале Чеддока с помощью эмпирического корреляционного отношения оценивается теснота связи между изучаемыми признаками.
Таблица 10.2
Шкала Чеддока
| Величина показателя тесноты связи по абсолютной величине | 0,1 - 0,3 | 0,3 - 0,5 | 0,5 - 0,7 | 0,7 - 0,9 | 0,9 - 0,99 |
| Характеристика связи | Сла бая | Умерен ная | Замет ная | Высокая (тесная) | Весьма высокая (очень тесная) |
Корреляционно-регрессионный анализ. Корреляционной связью между двумя признаками называется такая связь, при которой изменение среднего значения факторного признака вызывает изменение среднего значения результативного.
Конечная цель статистического изучения корреляционной связи состоит в получении статистической модели этой зависимости в форме уравнения регрессии или уравнения связи. Решение этой задачи осуществляется в следующей последовательности.
Осуществляется логический анализ сущности изучаемого явления и причинно-следственных связей, т.е. устанавливается результативный признак (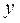
) и фактор (или факторы) его изменения (х1,х2,… 
). Связь двух признаков является парной корреляцией, а нескольких - множественной.
Проверка требований, предъявляемых к факторным и результативным признакам:
- однородность распределения, т.е. коэффициенты вариации не должны превышать 33 %: Vу ≤ 
, 
≤ 
;
- соответствие нормальному закону распределения, - чаще всего используется правило “трех сигм”.
Если 
и 
, то с вероятностью 0,997 можно утверждать, что распределение соответствующих признаков (ре-зультативного и факторного) соответствуют нормальному закону распределения.
независимость по объектам наблюдения. Если рассматривается статическое распределение или ряды распределения, то это требование подтверждается путем логического анализа, т.е. apriori. В то же время при построении регрессионных моделей по рядам динамики дополнительно необходимо проверять гипотезы об отсутствии автокорреляции и тенденции в рядах динами (стр.325-326. данного раздела);
отсутствие мультиколлинеарности между факторными признаками (при множественной корреляции), т.е.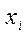 
и 
(
) не должны быть связаны между собой ни функциональной (мультипликативной или аддитивной), ни тесной корреляционной связью, т.е. 
или 
, k є 
; или 
≤ 0,8.
все факторные и результативные признаки должны иметь количественное выражение и взаимно соответствовать друг другу в пространстве, т.е. по объектам наблюдения, и по времени.
3. Исключение из массива первичной информации всех резко-выделяющихся (аномальных) единиц признаков-факторов и форми-рование нового массива для последующего анализа.
4. Определение формы и направления связи. В случае парных зависимостей применяются: содержательный анализ, графический метод, метод аналитических группировок и построение корреляцион-ных таблиц.
На основе данных аналитической группировки строится график эмпирической линии связи, вид которой не только позволяет судить о возможном наличии связи, но и дает некоторое представление о ее форме.
При построении корреляционных таблиц строится таблица взаимной сопряженности факторного и результативного признака, и по распределению частот можно предположить форму связи между ними (тема 2).
Реализация графического метода предполагает построение корреляционного поля, т.е. множества точек с координатами (
, 
, 
, 
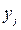- номер объекта наблюдения), в прямоугольной системе координат. По расположению точек (их плотности и направлению) можно судить о возможной форме связи между признаками.
При множественных зависимостях форма связи определяется путем содержательного анализа или по соотношению формальных критериев аппроксимации: из нескольких форм связи (линейная, степенная, логарифмическая и т.д.) выбирают тот вариант, для которого выполняется следующее соотношение критериев:
- 
- критерий метода наименьших квадратов;
- 
F –критерий – критерий Фишера-Снедскора;
- R 2 - максимальное значение множественного коэффициента детерминации.
5. Построение модели связи. На этом этапе определяются параметры уравнения связи по методу наименьших квадратов; - в результате чего строится система нормальных уравнений, решение которое и дает значение необходимых параметров (табл. 10.3).
6. Оценка тесноты связи. Для парных линейных зависимостей рассчитываются: линейный или парный коэффициент корреляции (rху), коэффициент детерминации (dху) и коэффициент эластичности (Кэл .) по следующим формулам: 
; 
= 
; Кэл .= 
.
Для нелинейных зависимостей, - теоретическое корреляционное отношение (
), коэффициент детерминации (
) и коэффициент эластичности (К эл .).
; = 
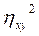; Кэл .= 
;
где 
- первая производная по уравнению связи.
7. Проверка статистической достоверности или существенности (значимости) показателей тесноты связи, уравнения связи и параметров уравнения связи.
Оценка достоверности парного коэффициента корреляции, корреляционного отношения и параметров линейного уравнения связи проводится на основе критерия Стьюдента:
- рассчитывается расчетное значение критерия (
):
- для показателей тесноты связи: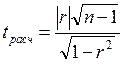 
или 
;
- для 
параметра уравнения связи: 
,
где 
.
Таблица 10.3
