1) определяются средние уровни с помощью математического урав-нения; 2) отыскиваются и сравниваются базисные темпы роста; 3) производится замена абсолютных данных средними арифметическими при постепенном исключении из рассмотрения первых уровней и включении последующих уровней; 4) производится замена абсолютных уровней данными.
Каким методом целесообразно сглаживать короткие динамические ряды?
1) с помощью скользящей средней; 2) путем укрупнения интервалов; 3) с помощью аналитического выравнивания; 4) исчислением средних по укрупненным интервалам.
Что является первым этапом аналитического выравнивания динамического ряда?
1) выявление характера динамики явления; 2) расчет выровненных уровней; 3) определение параметров уравнения по способу наименьших квадратов; 4) выбор математического выражения закономерности.
В каком случае упрощается система уравнений для нахождения параметров уравнения?
1) принимается четное количествоо периодов; 2) принимается нечетное количество периодов; 3) начало отсчета времени переносится в середину рассматриваемого периода; 4) расчет выполняется табличным методом.
По какой формуле можно определить?
1)  ; 2);
; 2); 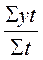 ; 3)
; 3)  4)
4)  .
.
В чем суть приема эмпирического сглаживания?
1) определяются средние уровни с помощью математического урав-нения; 2) отыскиваются и сравниваются базисные темпы роста; 3) про-изводится замена абсолютных данных средними арифметическими при постепенном исключении из рассмотрения первых уровней и включении последующих уровней; 4) производится замена абсолютных данных средними арифметическими за укрупненные периоды.
В чем суть метода наименьших квадратов?
1)  ; 2)
; 2) 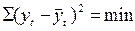 ; 3)
; 3)  ; 4)
; 4)  .
.
Какой расчет необходимо сделать для определения параметров уравнения?
1) 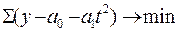 ; 2)
; 2)  ; 3)
; 3)  .
.
Какую систему уравнений надо решить для определения параметров уравнения?
1) 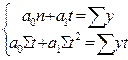 ;2)
;2)  ;3)
;3)  ;4)
;4) 
Решение типовых задач
Пример 1. Имеются следующие данные о товарных запасах торгового дома за 1994 – 2002гг., млн. грн.
1994 г. 1995 г. 1996 г. 1997 г. 1998 г. 1999 г. 2000 г. 2001 г. 2002 г.
10,0 10,7 12,0 10,3 12,9 16,3 15,6 17,8 18,0
Требуется выявить основную тенденцию изменения товарных запасов, используя следующие методы: 1) укрупнение интервалов времени; 2) эмпирическое сглаживание; 3) аналитическое выравнивание по прямой.
Решение
1. Укрупнение интервалов времени. Произведем укрупнение интервалов, начиная с объединения двух уровней:
1994-1995гг.:10,0+10,7=20,7 млн.грн; 1998-1999гг.:12,9+16,3=29,2 млн.грн
1996-1997гг.:12,0+10,3=22,3 млн.грн; 2000-2001гг.:15,6+17,8=33,4млн.грн.
По результатам проведенных расчетов проявляется тенденция роста изучаемого показателя. Используя полученные суммы по периодам, можно рассчитать ступенчатые средние. Для наглядности итоги расчетов оформим в таблице.
Таблица 8.2
Укрупнение интервалов времени и ступенчатые средние, исчисленные по данным о товарных запасах торгового дома за 1994 – 2002 гг.
| Интервалы времени | Суммы по периодам,млн.грн. | Ступенчатые средние,млн.грн. |
| 1994 – 1995 | 20,7 | 10,4 |
| 1996 – 1997 | 22,3 | 11,2 |
| 1998 – 1999 | 29,2 | 14,6 |
| 2000 – 2001 | 33,4 | 17,7 |
| - | 18,0 |
Ступенчатые средние наглядно отображают тенденцию роста товарных запасов торгового дома за 1994–2002гг.
2. Эмпирическое сглаживание. Сгладим данный ряд динамики по трехлетней скользящей средней, т.к. период колебаний запасов равен трем годам. Исчислим:
средний уровень за 1994-1996гг.:  млн.грн.;
млн.грн.;
средний уровень за 1995-1997гг.:  млн.грн.;
млн.грн.;
средний уровень за 1996-1998гг.:  млн.грн.
млн.грн.
и т.д. Результаты расчета трехлетней суммы и скользящей средней по периодам представим в таблице (табл. 8.3).
Таблица 8.3
Сглаживание динамического ряда товарных запасов за 1994 – 2002гг. с помощью трехлетней скользящей средней
| Годы | Товарные за-пасы,млн.грн. | Период сглаживания | Середин-ный год | 3х-летние сум-мы,млн.грн | 3х-летние скользящие средние,млн. грн |
| 1 | 2 | 3 | 4 | 5 | 6 |
| 10,0 | – | – | – | – | |
| 10,7 | 1994 - 1996 | 32,7 | 10,9 | ||
| 12,0 | 1995 - 1997 | 33,0 | 11,0 | ||
| 10,3 | 1996 - 1998 | 35,2 | 11,7 | ||
| 12,9 | 1997 - 1999 | 39,5 | 13,2 | ||
| 16,3 | 1998 - 2000 | 44,8 | 14,9 | ||
| 15,6 | 1999 - 2001 | 19,7 | 16,6 | ||
| 17,8 | 2000 - 2002 | 51,4 | 17,1 | ||
| 18,0 | – | – | – | – |
Таким образом, нами получен новый ряд динамики (гр. 4 и 6), в котором наблюдается тенденция роста запасов за исследуемый период времени.
3. Аналитическое выравнивание. При выборе функции, описывающей тенденцию, логический анализ динамического ряда должен опираться на графические изображение его. Нанесем на график приведенные данные. Ломаная кривая, отображающая фактические данные, позволяет выбрать в качестве функции, описывающей тренд, уравнение прямой (рис.8.1).
Уравнение прямой выражается формулой: 
где  значение выравненного ряда (теоретические уровни);
значение выравненного ряда (теоретические уровни);  и
и  - параметры уравнения прямой;
- параметры уравнения прямой;  показатель времени.
показатель времени.
|

Рис. 8.1. Товарные запасы торгового дома за 1994–2002гг.
Для нахождения параметров  и
и  необходимо решить систему нормальных уравнений:
необходимо решить систему нормальных уравнений: 
где у – фактические уровни ряда динамики; п – количество уровней.
Для упрощения расчетов в рядах динамики обозначают время так, чтобы начало отсчета времени приходилось на середину рассматриваемого периода. Если количество уровней четное, то условное обозначение показателя времени принимает вид:
Годы 1997 1998 1999 2000 2001 2002
t -5 -3 -1 +1 +3 +5
Если количество уровней нечетное, условное обозначение t имеет вид:
Годы 1996 1997 1998 1999 2000 2001 2002
t -3 -2 -1 0 1 2 3
Таблица 8.4






