Распределение студентов по успеваемости

Успеваемость (балл), х	Число сту- дентов, f	Накопленные частоты, S_нак	x f	x² f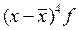
					88,875
					15,787
					0,086
					1,8136
					46,3333
Итого		-			152,8949

2. Графически дискретный вариационный ряд может быть представлен в виде полигона (рис.5.1), кумуляты (рис.5.2) распределения. Полигон строится в прямоугольной системе координат.

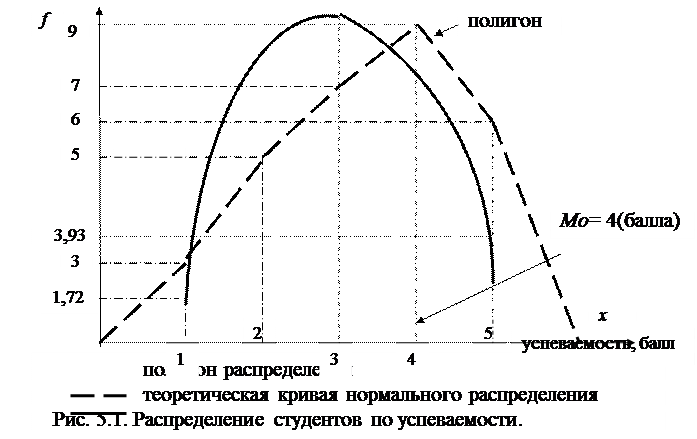По оси абсцисс откладываются значения дискретного признака, а по оси ординат – частоты распределения. Полигон часто замыкается, - для этого крайние вершины соединяются с точками на оси абсцисс, отстоящими на одно деление в принятом масштабе (в данном примере х = 0 и х = 6).

Кумулята – это линейный график накопленных частот. Для построения кумуляты дополнительно рассчитываются накопленные частоты (S_НАК), - они представлены в таблице 5.1, и в прямоугольной системе координат строится их график (рис.5.2).

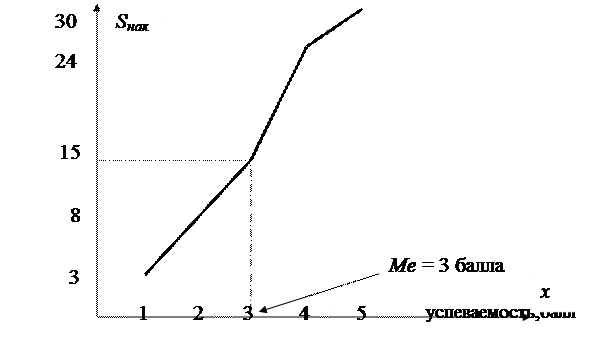Рис. 5.2. Кумулята распределения студентов по успеваемости

3. Cтруктурными средними выступают мода и медиана.

Модальное значение признака, т.е. М_о = 4 (балла). Графически – это вершина полигона распределения (рис.5.1).

Медиана равна 3 балла, так как S_НАК = 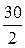=15 для признака, равному 3. Графически медиана определяется с помощью кумуляты распределения. Для ее определения сумму ординат (сумму частот) делят пополам, т.е. 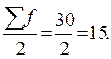. Через полученную точку проводится прямая параллельно оси абсцисс до пересечения ее с кумулятой. Абсцисса точки пересечения является медианной величиной распределения (рис. 5.2).

3. Для оценки формы распределения исчислим коэффициент асимметрии и эксцесса: 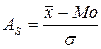; 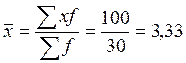(балла); М₀ =

= 4(балла); ; .

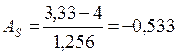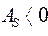, это свидетельствует о наличии левосторонней асимметрии распределения студентов по успеваемости (рис. 5.1).

Для проверки статистической гипотезы о существенности асимметрии рассчитываем соотношение 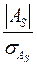, исчислив предварительно: = ; .

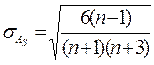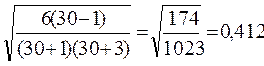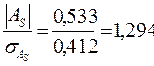
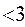В нашем примере наличие асимметрии несущественно и объясняется влиянием случайных факторов.

Исчислим коэффициент эксцесса: ; =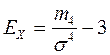

; .

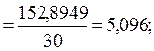
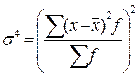
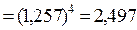Так как 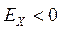, то распределение студентов по успеваемости – низковершинное или плосковершинное по сравнению с нормальным распределением.

5. Для проверки гипотезы о соответствии эмпирического распределения нормальному используем критерий Пирсона или - критерий. Определим теоретические частоты нормального распределения по формуле: 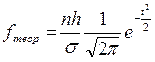; ; h = 1 (для дискретного ряда); n = ∑ f = 30, тогда .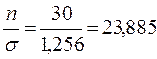

Все промежуточные расчеты представлены в таблице 5.2.

Определяем расчетное значение 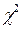-критерия: =2,1146. Полученное значение 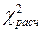=2,1146 сравнивается с табличным значением 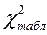, которое определяется по заданной вероятности (например, Р = 0,95) и числу степеней свободы (m = k – 3 = 5 - 2) (приложение 4).

Таблица 5.2

Вспомогательные расчеты теоретических частот нормального

закона распределения

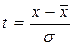
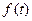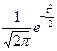
Успеваемость, (x)	Число студентов, (f)		[2]= =	Теор.частоты,	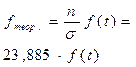Округл. теорет. частоты,
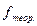
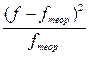
		-1,854	0,0721	1,72	2,0	0,5
		-1,058	0,2275	5,43	5,4	0,0296
		-0,262	0,3857	9,2	9,2	0,526
		0,533	0,3467	8,26	8,3	0,059
		1,328	0,1647	3,93	4,0	1,0
Итого					28,9[3]	2,1146

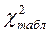= 6. Так как 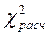< (2,1146 < 6,0), то гипотеза о соответствии эмпирического распределения нормальному с вероятностью 0,95 не отвергается. На рис.5.1 построим теоретическую линию нормального закона распределения. Эмпирическое распределение близко нормальному закону распределения, однако оно более плосковершинно, чем нормальное (Е_Х < 0) и с незначительной правовершинной асимметрией (А_S < 0), что видно на графическом изображении эмпирического и теоретического распределения.

Пример 2. Известно распределение коммерческих банков области по размеру прибыли.

Размер прибыли, млн.грн	До 10,0	10,0 – 20,0	20,0 - 30,0	30,0 - 40,0	40,0 - 50,0	Свыше 50,0	Ито- го
Количество банков

Оцените уровень вариации банков по размеру прибыли, рассчитав абсолютные и относительные показатели вариации. Сделайте выводы.

Решение

1. Для определения абсолютных показателей вариации необходимо закрыть открытые интервалы и перейти от интервального ряда к дискретному (табл.5.3. гр. 3)

Таблица 5.3

Вспомогательные расчеты для определения показателей вариации

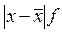
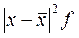
Размер прибыли,млн.грн	Количество банков, f	Середина интервала, х	xf			x²	x ² f
			4			7	8
до 10,0				52,5	1378,125
10,0-20,0					10562,5
20,0-30,0				156,25	976,5625
30,0-40,0				168,75	632,8125
40,0-50,0				687,5	9453,125
Свыше50,0				475,0	11281,25
Итого	200,0				46687,5

Рассчитываем следующие абсолютные показатели вариации: размах вариации (R); среднее линейное отклонение (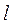), дисперсию (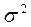) и среднее квадратическое отклонение( 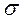). 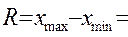60 – 0= = 60 (млн. грн.) Размер отклонений величины максимальной прибыли от минимальной по всей совокупности банков составляет 60 млн.грн.

Для расчета и определим средний размер прибыли по всей совокупности банков.

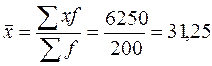млн.грн; 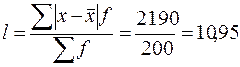млн.грн.

Индивидуальные размеры прибыли в среднем по всей совокупности банков отклонялись в ту и другую сторону от своего среднего значения на 10,95 млн. грн.

Дисперсию определим двумя способами:

- по формуле среднего квадрата отклонений = = 233,44

- по формуле “разности средних”: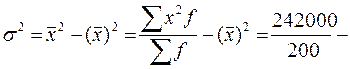

- (31,25) ²= 1210 – 976,56 = 233,44.

Среднее квадратическое отклонение: 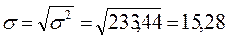млн.грн.

Размеры прибыли каждого из 200 банков отклонялись в ту и другую сторону от среднего значения на 15,28 млн. грн.

Определим теперь относительные показатели вариации:

- коэффициент осцилляции: ;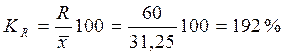

- относительное линейное отклонение: %;

- коэффициент вариации: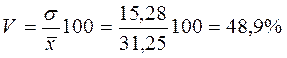

Анализируемый вариационный ряд распределения банков по размеру прибыли является статистически неоднородным, так как коэффициент вариации больше 33%. Об этом свидетельствует другие показатели вариации, например, коэффициент осциляции показывает, что разность между крайними значениями признака почти в 2 раза больше (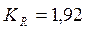 или 192 %) их среднего значения.

Среднее значение показателя прибыли по данной совокупности банков (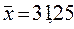 тыс.грн) не является надежной или типической ее характеристикой.

Пример 3. Распределение семей по среднедушевым доходам следующее (таблица 5.4). 1. Определите: а) структурные характерис-тики распределения семей по размеру среднедушевого дохода; б) показатели формы и дифференциации распределения. 2. Проверьте статистическую гипотезу о соответствии эмпирического распределе-ния нормальному. 3. Постройте график эмпирического и теоретичес-кого распределения семей по размеру среднедушевого дохода.

Решение

1а. Определяем структурные характеристики ряда распределе-ния, т.е. моду медиану, квартили, децили по рассмотренным выше формулам этих характеристик для интервальных вариационных рядов.

Для выбора соответствующего интервала предварительно опре-делим накопленные частоты 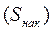, (табл. 5.4, гр. 4).

Модальный интервал – это интервал с наибольшей частотой 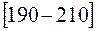, тогда грн.

Большинство семей имеют среднедушевые доходы в размере 196,67 грн. Медианным является интервал 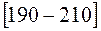, т.к. для него первая накопленная частота больше половины объема совокупности, т.е. 120>100. Тогда медиана будет равна: 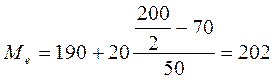грн.

Половина семей имеют среднедушевые доходы, не превышаю-щие доходы 202 грн., а у другой половины семей среднедушевые доходы, соответственно, выше 202 грн.

Интервал, в котором будет находиться первый квартиль(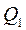) рас-пределения, , т.к. ему соответствует первая накопленная час-тота 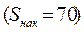, большая 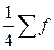; а интервал, в котором находится третий квартиль(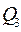), будет 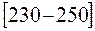, т.к. ему соответствует > .

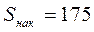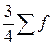Тогда соответствующие квартили будут равны:

грн; грн.

Среднедушевые доходы, не превышающие 180 грн., получают не менее четверти (25%) из всей совокупности семей, а в размере, не превышающем 230грн., не менее 75% всех семей.

Более детальная характеристика распределения может быть получена на основе децилей распределения. Интервалы соответствующих децилей определяются аналогично по соответствующим накопленным частотам. Например, находим первую 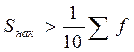, - это будет 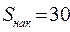; тогда соответствующий ей интервал 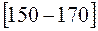будет тем интервалом, в котором находится первый дециль (d₁) – и т.д.

Рассчитаем соответствующие децили:

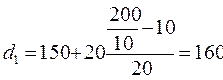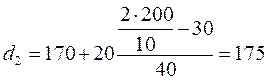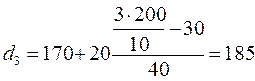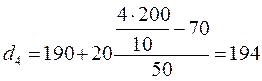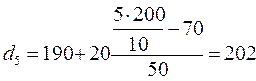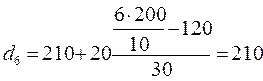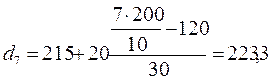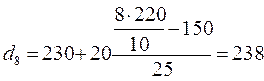грн; грн;

грн. Первый дециль показывает, что у 10% семей с самым низким среднедушевым доходом самый высокий размер среднедушевого дохода составляет 160 грн., а девятый дециль, - что среди 10% семей с самым высоким уровнем дохода – нижняя его граница составляет 254 грн.

1б. Анализ формы, дифференциации и концентрации распределения проводится с помощью системы специальных коэффициентов, в частности, рассчитываются:

- относительный показатель асимметрии (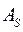), показатель эксцесса (), коэффициент децильной дифференциации (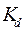), индекс Джинни (К^Дж).

Дополнительно используется графическое изображение степеней неравномерности распределения вариационного ряда в виде кривой Лоренца.

Относительный показатель асимметрии исчислим как:

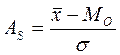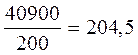; грн;

33,3 грн;

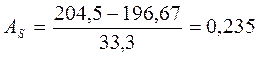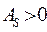, т.е. это свидетельствует о наличии правосторонней асим-метрии, при этом она незначительная, т.к. 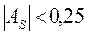. Наиболее точ-ным выступает коэффициент асимметрии, рассчитанный на основе третьего центрального момента:

; ;

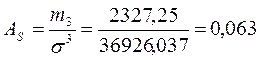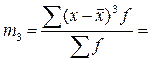
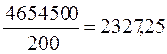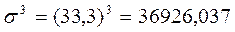
Для проверки существенности (или несущественности) асимметрии определяется средняя квадратическая погрешность коэффициента асимметрии(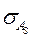): ; 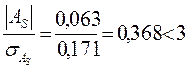,т.е.асим-метрия несущественна в данном вариационном ряду. Так как приведенное распределение симметричное, то для таких распределений дополнительно рассчитывается коэффициент эксцесса:

; ; ; .

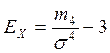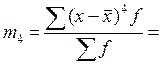
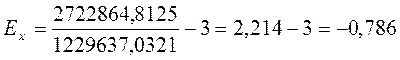Значение 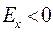свидетельствует о том, что распределение низко-вершинное или плосковершинное.

Для проверки гипотезы о статистической существенности эксцес-са рассчитываем среднеквадратическую ошибку эксцесса:

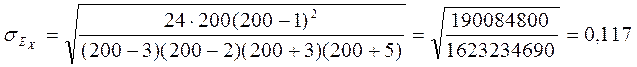_.Если 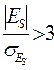, то гипотеза о статистической существенности экс-цесса не отвергается: 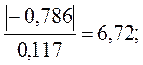т.е. 6,72 >3. Это подтверждает ги-потезу о статистической значимости (или существенности) эксцесса.

Для оценки степени дифференциации признака в совокупности рассчитаем коэффициент децильной дифференциации:

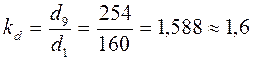
Это означает, что в 1,6 раза наименьший среднедушевой доход 10% семей, имеющих наибольшие доходы, больше наибольшего сред-недушевого дохода из 10% семей, имеющих самые низкие среднедуше-вые доходы.

Анализ дифференциации (или концентрации) распределения признаков основан на построении кривой Лоренца и расчета индекса дифференциации или коэффициента Джинни.

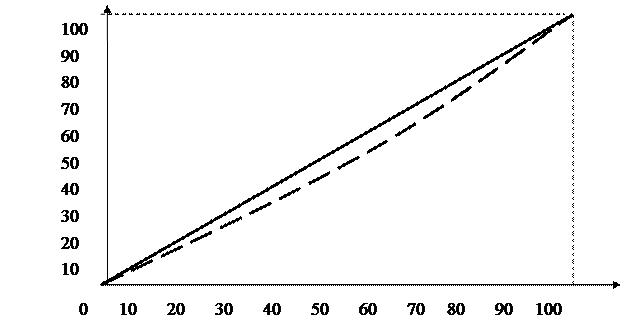
По данным таблицы 5.4 построим кумулятивные относительные показатели изучаемого признака (среднедушевого дохода) и частот (чис-ла семей), т.е. относительные показатели числа единиц в группах и раз-мерах признака (среднедушевые доходы) выражаются в относительных величинах (в долях или процентах к итогу) и определяются их накоп-ленные значения (табл.5.5, гр.5 и 8). Для построения кривой Лоренца по горизонтальной оси графика откладываются значения графы 5, а по вер-тикальной - значения графы 8, и соединение этих точек образует кривую Лоренца, характеризующую равномерность и степень концентрации распределения рабочих по уровню среднедушевого дохода (рис. 5.3).

fсиm,%

Рис.5.3. Кривая Лоренца

Для количественной оценки меры концентрации рассчитывает-ся коэффициент концентрации Джинни:

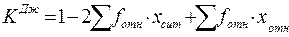= 1 – 2 · 0,538015 + 0,1500335 = 0,074.

Соотношение линий равномерного и фактического распределения (рис.5.3), а также значение коэффициента близкое к 0, свидетельствует о достаточно равномерном распределении семей по среднедушевомудоходу и, соответственно, о незначительной степени концентрации.

2. Проверяем гипотезу о соответствии эмпирического распределения семей по среднедушевому доходу нормальному закону распределения, используя критерий согласия К. Пирсона или χ² - критерий.

Таблица 5.4

Распределение семей по среднедушевому доходу

Среднеду-шевые доходы, грн	Число се- мей	Закрытые ин-тервалы сред-недушевых доходов, грн		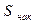х	xf	x ² f
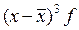
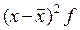
1	2	3	4	5	6	7	8	9	10	11
До 150,0		130 - 150					- 64,5	- 2683361,25	173076800,625	41602,5
150,0 -170,0		150 - 170					- 44,5	-1762422,5	78427801,25
170,0 -190,0		170 - 190					- 24,5	- 588245	14412002,5
190,0 -210,0		190 - 210					- 4,5	- 4556,25	20503,125	1012,5
210,0 -230,0		210 - 230					15,5	111716,25	1731601,875	7207,5
230,0 -250,0		230 - 250					35,5	1118471,875	33705751,625	31506,25
Свыше 250,0		250 - 270					55,5	4273846,975	237198501,5625	77006,25
Итого								465450,0	544572962,5

Таблица 5.5