1) 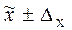 ; 2)
; 2)  ; 3)
; 3)  ; 4)
; 4) 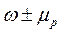 .
.
По какой формуле определяются пределы генеральной доли?
1) 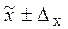 ; 2)
; 2) 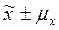 ; 3)
; 3)  ; 4)
; 4) 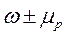 .
.
Какие ошибки не специфичны для выборочного наблюдения?
1) ошибки регистрации преднамеренные; 2) ошибки регистрации не-преднамеренные; 3) случайные ошибки репрезентативности; 4) пре-дельная ошибка выборки.
Как изменится средняя ошибка выборки при повторном отборе, если объем выборки увеличить в четыре раза?
1) уменьшится в 4 раза; 3) увеличится в 2 раза;
2) уменьшится в 2 раза; 4) увеличится в 4 раза.
Какой способ отбора является наиболее точным?
1) собственно-случайный; 3) типический;
2) механический; 4) серийный.
Чему равна средняя ошибка выборочной доли при случайном бесповторном отборе?
1) 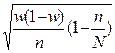 ; 2)
; 2) 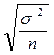 ; 3)
; 3)  ; 4)
; 4) 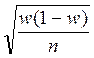 .
.
По какой формуле определяется предельная ошибка выборки для признака при механическом отборе?
1) 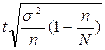 ; 2)
; 2) 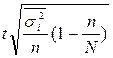 ; 3)
; 3) 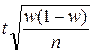 ; 4)
; 4) 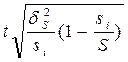 .
.
Какая формула положена в основу определения необходимого объема выборочной совокупности при собственно-случайном повторном отборе?
1) 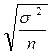 ; 2)
; 2)  ; 3)
; 3) 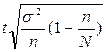 ; 4)
; 4) 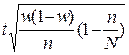 .
.
Как определяется предельная ошибка доли при типическом отборе?
1) 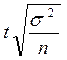 ; 2)
; 2) 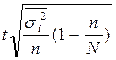 ; 3)
; 3) 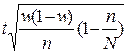 ; 4)
; 4) 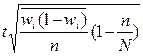 .
.
По какой формуле определяется предельная ошибка выборки для признака при серийном повторном отборе?
1) 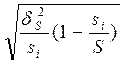 ; 2)
; 2) 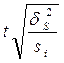 ; 3)
; 3)  ; 4)
; 4) 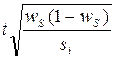 .
.
Решение типовых задач
Пример 1. Для изучения оснащения заводов основными производственными фондами было проведено 10%-ное собственно-слу-чайное обследование, в результате которого получены следующие данные о распределении заводов по стоимости фондов:
| Средняя годовая стоимость основных фондов, млн. грн | До 4 | 4 - 6 | 6 - 8 | Свыше 8 | Итого |
| Количество заводов |
Определите: 1) с вероятностью 0,997 границы, в которых будет находиться средняя годовая стоимость основных фондов заводов в генеральной совокупности; 2) с вероятностью 0,954 границы, в которых будет находиться удельный вес заводов со стоимостью фондов выше 6 млн.грн. в генеральной совокупности.
Решение
1. Средняя годовая стоимость основных фондов в генеральной совокупности определяется по формуле: 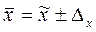 .
.
Предельная ошибка рассчитывается так: 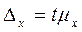 .
.
При собственно-случайном бесповторном отборе  определяется по формуле:
определяется по формуле: 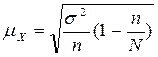 . Для расчета средней и дисперсии по выборочной совокупности построим таблицу 6.3.
. Для расчета средней и дисперсии по выборочной совокупности построим таблицу 6.3.
Таблица 6.3
Вспомогательные расчеты для определения средней и
дисперсии по результатам выборки
| Средняя годовая стоимость основных фондов, млн. грн | Кол-во заводов | Дискрет
ный ряд, 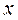
|
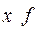
|
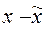
|
(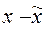 )2 )2
|
(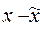 )2 f )2 f
|
| До 4 | - 3,4 | 11,56 | 80,92 | |||
| 4 – 6 | - 1,4 | 1,96 | 23,52 | |||
| 6 – 8 | 0,6 | 0,36 | 7,56 | |||
| Свыше 8 | 2,6 | 6,76 | 67,60 | |||
| Итого: | - | - | - | 179,60 |
Средняя в вариационном ряду, т.е. по выборочной совокупнос-ти, рассчитывается следующим образом: 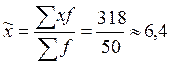 млн.грн.
млн.грн.
Дисперсию определим по формуле: 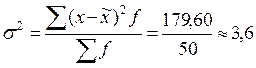 .
.
N = 500, т. к. по условию задачи объем выборки составляет 10% от генеральной совокупности (n = 50). Тогда средняя ошибка выборки составит: 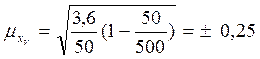 млн.грн.
млн.грн.
В нашем примере задана вероятность 0,997, при которой 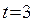 , и предельная ошибка выборки будет равна:
, и предельная ошибка выборки будет равна: 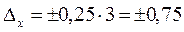 млн.грн.
млн.грн.
Средняя годовая стоимость основных фондов в генеральной совокупности будет находиться в пределах:
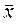 = 6,4млн.грн.
= 6,4млн.грн. 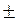 0,75 млн.грн; 5,65 млн.грн
0,75 млн.грн; 5,65 млн.грн 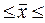 7,15млн.грн.
7,15млн.грн.
Следовательно, с вероятностью 0,997 можно утверждать, что средняя годовая стоимость основных фондов в генеральной совокупности будет находиться в пределах от 5,65 до 7,25 млн.грн.
2.Доля заводов со стоимостью основных фондов свыше 6 млн.грн в генеральной совокупности определяется по формуле: 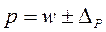 .
.
Доля таких заводов в выборочной совокупности будет следующей:  ;
; 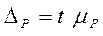 .
.
В нашем примере задана вероятность 0,954, поэтому 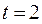 .
.
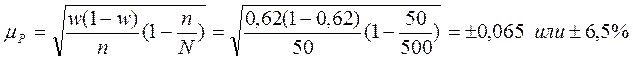

Тогда доля заводов, имеющих стоимость основных фондов свыше 6 млн.грн., в генеральной совокупности составит:
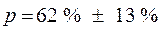 ;
; 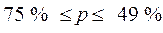 .
.
Таким образом, доля заводов со стоимостью основных фондов свыше 6 млн.грн во всей генеральной совокупности будет находиться в пределах от 49 до 75%. Результат гарантируется с вероятностью 0,954.
Пример 2. Для определения средней месячной заработной платы работников финансово-банковских учреждений было проведено выборочное обследование 100 сотрудников по схеме собственно-слу-чайного повторного отбора. В результате установлено, что средняя зарплата составляет 880 грн. при среднем квадратическом отклонении 169 грн. С вероятностью 0,954 определите пределы, в которых находится средняя зарплата в генеральной совокупности.
Решение
Средняя зарплата работников в генеральной совокупности будет определяться по формуле: 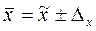 . Для определения границ генеральной средней необходимо вычислить предельную ошибку выборки:
. Для определения границ генеральной средней необходимо вычислить предельную ошибку выборки: 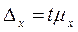 ;
; 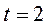 ;
; 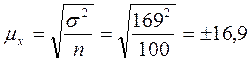 грн.;
грн.; 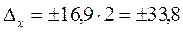 грн;
грн; 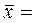 880 ± 33,8; 846,2 грн.
880 ± 33,8; 846,2 грн. 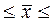 913,8 грн.
913,8 грн.
С вероятностью 0,954 можно утверждать, что средняя зарплата работников финансово-банковских учреждений в генеральной совокупности находится в пределах от 846,2 до 913,8 грн.
Пример 3. В процессе осуществления технического контроля из партии готовой продукции методом случайного бесповторного отбора было проверено 80 изделий, из которых 4 оказались бракованными. С вероятностью 0,954 определите пределы бракованной продукции во всей, если процент отбора равен 10.
Решение
Доля бракованной продукции в генеральной совокупности будет находиться по формуле:  . Определим процент бракованной продукции в выборочной совокупности:
. Определим процент бракованной продукции в выборочной совокупности: 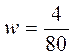 = 0,05 или 5 %.
= 0,05 или 5 %.
Предельная ошибка выборки определяется так: 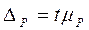 ,
,
где 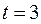 при заданной в условии задачи вероятности.
при заданной в условии задачи вероятности.
Средняя ошибка выборки составит:
 или ± 2,3 %.
или ± 2,3 %.
 .
.
Тогда доля бракованной продукции в генеральной совокупности будет следующей: 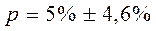 ;
; 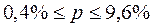 .
.
С вероятностью 0,954 можно утверждать, что доля брака во всей партии готовой продукции будет находиться в пределах от 0,4 до 9,6%.
Пример 4. Для определения средней заработной платы продавцов в регионе была произведена 20 %-ная типическая выборка с отбором единиц пропорционально численности типических групп (внутри типов применялся метод случайного бесповторного отбора). Результаты выборки представлены в таблице:
| Типические группы магазинов | Средняя заработная плата, грн, х | Среднее квадратическое отклонение, грн, 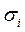
| Число про-давцов, 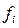
|
| Продовольственные Непродовольственные |
С вероятностью 0,954 определите предел, в котором будет находиться средняя заработная плата всех продавцов в регионе.
Решение
Пределы генеральной средней определяются по формуле: 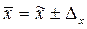
Определим среднюю в выборочной совокупности:
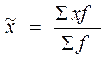 =
=  грн.
грн.
Средняя ошибка выборки при типическом способе отбора для средней величины признака рассчитывается так: 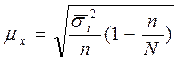 .
.
Определим среднюю из групповых дисперсий:
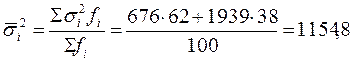 ;
; 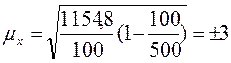 грн.
грн.
Тогда предельная ошибка выборки составит:
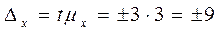 грн
грн
Следовательно, средняя зарплата продавцов в генеральной совокупности с вероятностью 0,954 будет находиться в пределах:
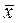 = 360,4 ± 9,0; 351,4 грн.
= 360,4 ± 9,0; 351,4 грн.  369,4 грн.
369,4 грн.
Пример 5. Для выявления причин простоев была произведена фотография рабочего дня 10% рабочих трех цехов завода. Отбор рабочих внутри цехов производился механическим способом. В результате была выявлена такая доля простоев из-за несвоевременного поступления материалов к рабочему месту:
| Цеха | Число рабочих
в выборке, 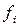
| Удельный вес простоев из-за несвоевременного поступления материалов 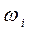
|
| 0,10 0,15 0,02 |
С вероятностью 0,954 определите пределы, в которых находится доля простоев на заводе из-за несвоевременного поступления материалов.
Решение
Доля в генеральной совокупности определяется так: 
Рассчитаем выборочную долю простоев:
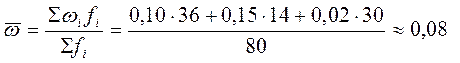 или 8 %.
или 8 %.
Определим дисперсии типических групп:
для 1 цеха: 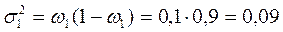 ;
;
для 2 цеха: 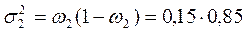 = 0,1275;
= 0,1275;
для 3 цеха: 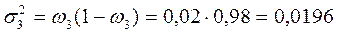 .
.
Средняя из групповых дисперсий будет равна:
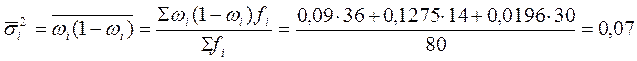
Определим среднюю ошибку выборочной доли:
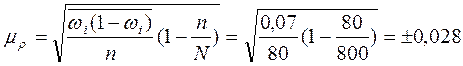 или 2,8 %.
или 2,8 %.
Рассчитаем предельную ошибку выборочной доли: 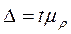 =
=
±2,8%· 2= ± 5,6 %. Тогда доля простоев с вероятностью 0,954 в генеральной совокупности будет находиться в пределах:
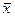 = 8 % ± 5,6 %;
= 8 % ± 5,6 %; 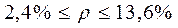
Пример 6. С целью прогнозирования урожая пшеницы в хозяйстве была проведена 5%-я серийная выборка посевных площадей этой культуры, в которую попали три участка. В результате обследования установлено, что средняя урожайность пшеницы на участках составила 28, 32, 30 ц/га. С вероятностью 0,954 определите пределы, в которых будет находиться средняя урожайность пшеницы в хозяйстве.
Решение
Средняя в генеральной совокупности рассчитывается по формуле: 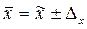 .Определим среднюю по выборке:
.Определим среднюю по выборке: 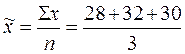 =30 ц/га
=30 ц/га
Межсерийная дисперсия, необходимая для расчета средней ошибки выборки, будет следующей:
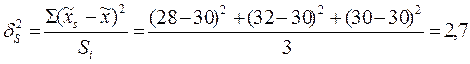 .
.
Тогда предельная ошибка серийной выборки (t =2, т.к. P = 0,954) составит: 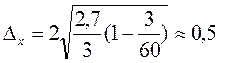 ц/га.
ц/га.
Следовательно, средняя урожайность в хозяйстве будет находиться в пределах: 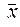 = 30 ± 0,5; 29,5ц
= 30 ± 0,5; 29,5ц 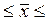 30,5ц. Результат гарантирован с вероятностью 0,954.
30,5ц. Результат гарантирован с вероятностью 0,954.
Пример 7. С целью определения доли сотрудников коммерческих банков в возрасте старше 40 лет предполагается организовать типическую выборку пропорционально численности сотрудников мужского и женского пола с механическим отбором внутри групп. Общее число сотрудников банков составляет 13 тыс.чел., в т.ч. 8 тыс. мужчин и 5 тыс.женщин. На основании предыдущих обследований известно, что средняя из групповых дисперсий доли составляет 600. Определите необходимый объем выборки при вероятности 0,997 и ошибке.
Решение
 чел.
чел.
Объем предельных типических групп при этом составит:
мужчины - 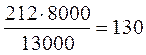 чел.; женщины -
чел.; женщины -  чел.
чел.
Таким образом, необходимый объем выборочной совокупности сотрудников коммерческих банков составляет 212 чел., в т.ч. 130 мужчин и 82 женщины.






