| Среднедушевой доход, грн. | Число семей | Общая сумма среднемесячных доходов |
|
| |||||
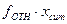
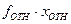
| интервальное распределение | диск- ретное, х | кол-во семей, f | частость, %, fотн, | накоплен- ная частость, %, fcum, | гри- вен, xf | в % к итогу xотн | накоплен- ный % к итогу, xcum | ||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 130 - 150 | 5,0 | 3,42 | 3,42 | 0,00171 | 0,00171 | ||||
| 150 - 170 | 7,82 | 11,24 | 0,01124 | 0,00782 | |||||
| 170 - 190 | 17,6 | 28,84 | 0,05768 | 0,0352 | |||||
| 190 - 210 | 24,45 | 53,29 | 0,133225 | 0,061125 | |||||
| 210 - 230 | 16,1 | 69,39 | 0,104085 | 0,02415 | |||||
| 230 - 250 | 12,5 | 87,5 | 14,67 | 84,06 | 0,105075 | 0,0183375 | |||
| 250 - 270 | 12,5 | 15,94 | 0,125 | 0,0019925 | |||||
| Итого: | - | - | - | 0,538015 | 0,1500335 |
Таблица 5.6
Вспомогательная таблица для расчета теоретических частот
Нормального распределения
| Средне душевые доходы, грн. | Число семей, f | x |
| 
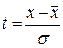
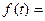
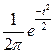
| Теоретические частоты, fтеор | Округленные частоты, fтеор |
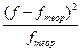
| Накопленные частоты | Разность между накопленными фактическими и теоретическими частотами | |
| фактически | теоретически | |||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 = 9 - 10 |
| 130 - 150 | -1,937 | 0,062 | 7,4462 | 7,4 | 0,9135 | 7,4 | - 2,6 | |||
| 150 - 170 | -1,336 | 0,1646 | 19,768 | 19,8 | 0,00202 | 27,2 | - 2.8 | |||
| 170 - 190 | - 0,7357 | 0,3040 | 36,63 | 36,6 | 0,3158 | 63,8 | 6,2 | |||
| 190 - 210 | 0,1351 | 0,3954 | 47,49 | 47,5 | 0,1316 | 111,3 | 8,7 | |||
| 210 - 230 | 0,4655 | 0,3585 | 43,056 | 43,0 | 3,93 | 154,3 | 4,3 | |||
| 230 - 250 | 1,066 | 0,240 | 29,06 | 29,1 | 0,578 | 183,4 | - 8,4 | |||
| 250 - 270 | 1,667 | 0,1000 | 12,06 | 12,1 | 13,75 | 195,5 | 4,5 | |||
| Итого | 195,5' | 19,62 |
Этапы решения:
- определяем теоретические частоты нормального закона распределения (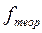
) по формуле: 
; 
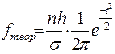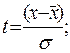
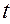-нормированное отк-лонение; 
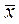= 204,5 грн; 
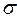= 33,3. (Все промежуточные расчеты представлены в таблице 5.6). Общий множитель 
;
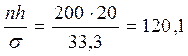- по таблицам t- распределения (приложение 3) определяем значение плотности: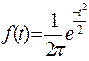 
,при этом 
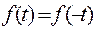. Например, для 
; 
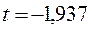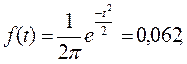для 
; 
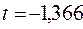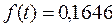и т.д. Эти значения заносятся в графу 5 таблицы 5.6;
- определяем теоретические частоты (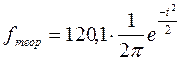
) и заносим их в графу 6, а округленные – в графу 7 таблицы 5,6; сумма теоретических частот 
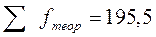, т.е. несколько меньше 200, что объясняется округлением цифр при расчете f (t) и f теор.
Для оценки степени расхождения эмпирического и теоретического распределения используется критерий Пирсона (промежуточные расчеты представлены в графе 8 табл. 5.6)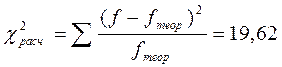 
.
Определяем табличное значение критерия, т.е.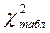 
по заданной вероятности (
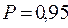или 0,9) и числу степеней свободы: 
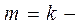3=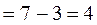 
(см. приложение 4).
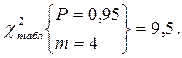Т.к.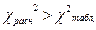 
, то гипотеза о соответствии эмпирического распределения нормальному закону распределения не подтверждается.
Для проверки этой же статистической гипотезы можно использовать критерий Романовского и критерий Колмогорова.
- Критерий Романовского: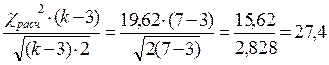 
. Если 
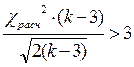, то гипотеза о соответствии эмпирического распределения нормальному не принимается.
- Критерий Колмогорова: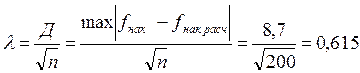 
.
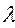- распределения определяет вероятность, т.е. 
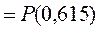= = 0,15 (приложение 5).
Если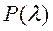 
- значительна, т.е. близка к 1, то расхождения между эмпирическим и нормальным распределением несущественны. В нашем примере расхождения существенны, что подтверждает сделанные выше выводы.
3. Построим графики эмпирического и теоретического распределения семей по среднедушевым доходам (рис.5.4):
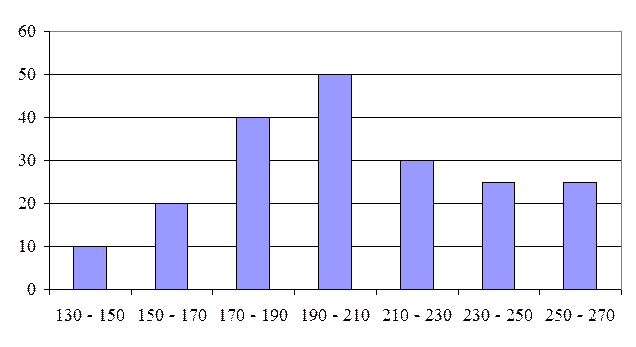- гистограмма распределения
- 
полигон распределения
- 
теоретическая линия нормального распределения
Рис.5.4. Распределение семей по среднедушевому доходу
Пример 5. Налоговой инспекцией одного из районов города проверено 172 коммерческих киоска и в 146 из них выявлены финансовые нарушения. Определите среднее значение, дисперсию и среднее квадратическое отклонение альтернативного признака, т.е. доли киосков, у которых выявлены финансовые нарушения.
Решение
Определяем долю коммерческих киосков, у которых выявлены финансовые нарушения: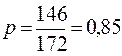 
. Тогда доля киосков, у которых отсутствуют финансовые нарушения, будет: 
.
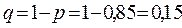Среднее значение альтернативного признака: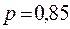 
. Дисперсия альтернативного признака составит: 
= 0,85 · 0,15 = 0,128, а среднее квадратическое отклонение: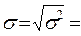 
.
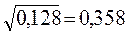Пример 6. Имеется следующая аналитическая группировка зависимости средней заработной платы рабочих от возраста.
| Группы ра-бочих по возрасту,лет | Число рабо- чих, fi | Средняя заработная плата, грн, у | 
| 
|
| до 20,0 | 280, 320, 360, 350, 290 | |||
| 20,0 – 30,0 | 420, 400, 510, 490, 380, 440, 480,500 | |||
| 30 и старше | 570, 600, 680, 630, 560, 440, 620 | |||
| всего |
Определите: 1) общую, межгрупповую и среднюю из внутригрупповых дисперсий; 2) проверьте правило сложения дисперсий.
Решение
1. Общая дисперсия по заработной плате рассчитывается по формуле простой дисперсии: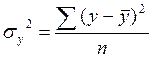 
.
где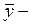 
средняя заработная плата всех рабочих;
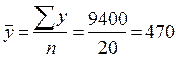грн
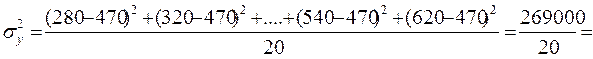13450
Межгрупповая дисперсия:
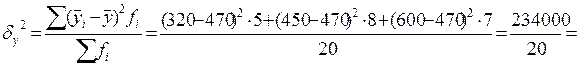11700,
где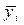 
- средняя зарплата по i -группе, представлены в таблице.
Средняя из внутригрупповых дисперсий. Вначале рассчитываем дисперсии по каждой группе:
;
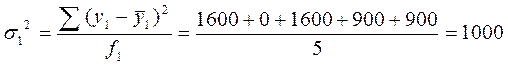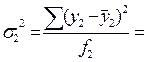
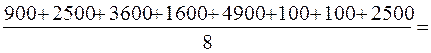2025;
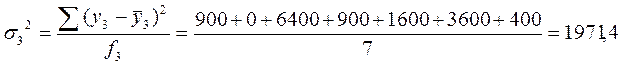
Тогда средняя из внутригрупповых дисперсий будет:
.
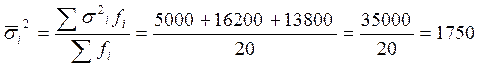2. Правило сложения дисперсий: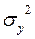 
= 
+ 
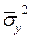;13450 = 11700 + 1750.
