1) размах вариации; 3) мода;
2) среднее линейное отклонение; 4) дисперсия.
Какой показатель можно определить по формуле:?
1) размах вариации; 2) дисперсию;3) среднее линейное отклонение простое; 4) среднее квадратическое отклонение взвешенное.
3. Укажите формулу упрощенного способа расчета дисперсии:
1) 
; 2) 
; 3) 
; 4) 
.
Какой показатель применяется для характеристики формы распределения?
1) коэффициент вариации; 3) децильные коэффициенты;
2) коэффициент асимметрии; 4) коэффициент Джинни.
Что характеризуют с помощью коэффициента эксцесса?
1) степень однородности распределения; 2) плоско или островер-шинность распределения; 3) дифференциацию распределения; 4) асимметричность распределения;
Какой показатель не характеризует структуру распределения вариационного ряда?
1) децили; 2) квартили; 3) медиана; 4) размах вариации.
Что характеризует коэффициент вариации?
1) чаще всего встречающийся признак в совокупности; 2) степень однородности совокупностей, достоверность средней; 3) средний квадрат отклонений признаков от средней величины; 4) крайние отклонения признака.
Какой показатель определяется по формуле?
1) среднее линейное отклонение; 2) размах вариации; 3) дисперсия альтернативного признака; 4) средняя альтернативного признака.
Какое соотношение лежит в основе -критерия Пирсона?
1) 
; 2) 
; 3) 
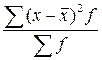; 4) 
.
Какой критерий не применяется для проверки гипотезы о соответствии эмпирического распределения нормальному закону распределения?
1) 
-критерий; 2) критерий Колмогорова; 3)критерий “существенности разности средних”; 4) коэффициент асимметрии и эксцесса.
Какой показатель определяется по формуле?
1) общая дисперсия; 3) межгрупповая дисперсия;
2) средняя из групповых дисперсий; 4) коэффициент асимметрии.
Какая формула применяется для оценки децильной дифференциации распределения?
1) 
; 2) 
; 3) 
; 4) p q.
Какой показатель определяется по формуле:?
1) общая дисперсия; 2) средняя из внутригрупповых дисперсий;
3) межгрупповая дисперсия; 4) коэффициент асимметрии.
При каких условиях структурные средние совпадают?
1) ряд распределения имеет левостороннюю асимметрию; 2) эмпи-рическое распределение соответствует нормальному закону распре-деления; 3) эмпирическое распределение более островершинное, чем кривая нормального распределения.
Каким может быть максимальное значение дисперсии альтернативного признака?
1) 0,5; 2) 0,25; 3) 0,09; 4) 1
Решение типовых задач
Пример 1. Имеются следующие данные об успеваемости студентов факультета по статистике: 4, 2, 5, 5, 3, 4, 3, 2, 5, 5, 4, 4, 3, 3, 4, 2, 1, 1, 1, 3, 4, 4, 4, 5, 5, 4, 2, 2, 3, 3.
Для анализа распределения студентов по успеваемости: 1) постройте дискретный ряд распределения; 2) дайте графическое изображение ряда; 3) исчислите структурные средние ряда (двумя способами) и показатели формы распределения; 4) проверьте гипотезу о соответствии эмпирического распределения нормальному закону распределения.
Решение
1. Для построения дискретного вариационного ряда необходимо подсчитать количество появления каждой оценки, т.е. частоту появления признака. Дискретный ряд представлен в таблице 5.1.
Таблица 5.1
