СТАТиСТИЧЕСКАЯ ПРОВЕРКА ГИПОТЕЗ
Методические указания
1. Анализ рядов распределения. Упорядоченное распределение единиц совокупности по определенному варьирующему признаку представляет собой ряд распределения.
Первым этапом статистического изучения вариации количественного признака является построение вариационного ряда, который в зависимости от характера представления варьирующего признака может быть: а) интервальным; б) дискретным. Если же признак атрибутивный или альтернативный, то, соответственно, строятся атрибутивный или альтернативный ряды распределения.
Графически вариационный ряд изображают в виде полигона и гистограммы. Они дают представление о характере и форме распределения варьирующих признаков в совокупности, при этом в случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения.
Процессы концентрации или неравномерности распределения (концентрация производства, концентрация капитала и др.) изображаются графически в виде кривой Лоренца. Для ее построения абсолютные значения частот и размер изучаемого признака выражаются в относительных показателях (в долях или процентах к итогу) и исчисляются их накопленные значения. На оси “ х ” наносится шкала накопленных частостей, на оси “ у ” - накопленные значения варьирующего признака. Соединив все точки прямыми линиями, получают кривую Лоренца, которая по степени отклонения от диагонали характеризует степень неравномерности распределения признака (рис.5.3, пример 4).
Для анализа вариационных рядов используется три группы показателей:
- структурные характеристики ряда распределения;
- показатели меры вариации;
- показатели формы распределения.
Структурные характеристики ряда распределения. К ним от-носятся медиана (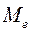
),мода (
), квартили (
), децили (
) и пер-центили (
) распределения.
Медиана – это величина варьирующего признака, которая делит ряд распределения на две равные части, т.е. медиана соответствует варианте, стоящей в середине ряда.
Медиана определяется в зависимости от вида ряда распределения:
- в ранжированном ряду с нечетным числом уровней медиана соответствует признаку с порядковым номером: 
,
где n - объем совокупности.
- в ранжированном ряду с четным числом значений варьирующего признака (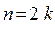
; 
) за медиану условно принимают значение: 
- в дискретном ряду распределения медиана соответствует варианте, для которой первая накопленная частота больше половины общего числа наблюдений;
- в интервальном ряду распределения медианным интервалом будет интервал, для которого первая накопленная частота больше половины объема совокупности, а сама медиана определяется по формуле: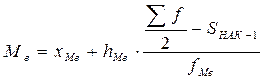 
,
где 
- нижняя граница медианного интервала; 
- величина медианного интервала; 
- частота медианного интервала; 
- накопленная частота до медианного интервала.
Графически медиана определяется по кумуляте распределения (рис. 5.2, пример 1).
Мода - наиболее часто встречающийся признак в совокупности. Определяется:
- в дискретном ряду – по максимальной частоте;
- в интервальном ряду модальный интервал определяется по максимальной частоте, а сама мода - по формуле:
,
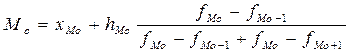где 
- нижняя граница модального интервала; 
- величина модального интервала; 
- частота модального интервала; 
- час-тота интервала, предшествующего модальному;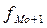 
- частота интервала, следующего за модальным.
Графически мода определяется на основе полигона распределения (для дискретного вариационного ряда) или гистограммы распределения (для интервального вариационного ряда) (рис.5.1, пример 1).
Значения признака, делящие совокупность на четыре равные части, называются квартелями и обозначаются буквой Q с подписным значком номера квартиля, - ясно, что Q2 совпадает с медианой, т.е. Q2 = = М е. Первый (Q 1) и третий (Q 3) квартили определяются по следующим формулам: 
; 
,
где хQ1,хQ3 - нижняя граница, соответственно, первого и третьего квартильных интервалов; hQ1, hQ3 - величина соответствующего первого и третьего квартильных интервалов; fQ1, fQ3 - частота соотвествующих квартильных интервалов; 
- накопленная частота до первого квартильного интервала;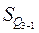 
- накопленная частота до третьего квартильного интервала.
Децили – варианты, делящие ряд распределения на десять равных частей. Вычисляются они по той же схеме, что и медиана, и квартили: 
; 
и т.д
Значения признака, делящее ряд на сто частей, называются перцентилями, и их расчет выполняется аналогично исчислению децилей и квартилей. Анализ вариационного ряда дополняется определением показателей дифференциации и концентрации. Например, коэффициент децильной дифференциации: 
,
где d9 – девятая дециль, или девятый дециль; d1 – первая дециль, или первый дециль.
Он показывает, во сколько раз наименьший уровень признака из 10% признаков, имеющих наибольший уровень, больше наибольшего уровня признака из 10% единиц совокупности, имеющих наименьший уровень признака.
Коэффициент фондов (Кф)– это соотношение между средними значениями изучаемого признака (или суммарными их значениями) в десятой и первой децильных группах, - рассчитывается по формуле: 
Более точной мерой степени дифференциации (или концентрации) является коэффициент Джини (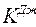
): 
.
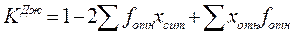где fотн - доля частот i- той группы; 
- доля признака i- той груп-пы; 
- кумулятивная доля признака.
Коэффициент Джини изменяется в пределах от 0 до 1, - чем ближе он к 1, тем выше уровень неравенства (концентрации) распределения, т.е. тем в большей степени варьирующий признак сконцентрирован в отдельной группе распределения, и наоборот.
Показатели меры вариации. Количественная оценка степени ко-леблемости признака в совокупности измеряется с помощью показателей вариации. Различают абсолютные и относительные показатели вариации.
Абсолютные показатели вариации:
1. Размах вариации: 
,
где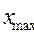 
, 
- соответственно, наибольшее и наименьшее значение варьирующего признака.
2. Среднее линейное отклонение:
- простое; 
- взвешенное.
3. Дисперсия:
- простая; 
- взвешенная.
4. Среднее квадратическое отклонение:
- простое;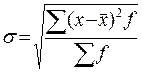 
- взвешенное.
Среднее квадратическое отклонение и среднее линейное отклонение – это обобщающие характеристики размеров вариации признака в совокупности, они выражаются в тех же единицах измерения, что и сам признак.
При сравнительно простых значениях признака используется упрощенный способ расчета дисперсии и среднего квадратического отклонения – метод разности средних: 
; 
.
- по несгруппированным данным: 
; 
,
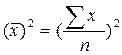- по сгруппированным данным: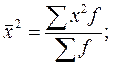 
Относительные показатели вариации:
- Относительный размах вариации или коэффициент осцилляции (КR): 
;
- Относительное линейное отклонение или линейный коэффициент вариации (К 
): 
;
- Коэффициент вариации (V):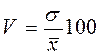 
.
Средняя и дисперсия альтернативного признака. Введем условные обозначения для альтернативного признака и построим альтернативный ряд распределения.
Альтернативный признак принимает значение 1, что означает наличие признака; 0 – его отсутствие; р – доля единиц, обладающих данным признаком, q – соответственно, необладающих данным признаком. Тогда среднее значение альтернативного признака будет равно: 
при этом p + q = 1, т.е. q =1 – p.
Дисперсия и среднее квадратическое отклонение рассчитываются по соотношению: 
.
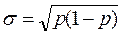Виды дисперсий и их взаимосвязь. При проведении группировки изучаемой совокупности по факторному признаку (х) вариацию результативного признака (у) можно оценить с помощью 3-х видов дисперсии:
- общей дисперсии (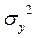
);
- межгрупповой дисперсии (
);
- средней из внутригрупповых дисперсий (
).
Общая дисперсия характеризует вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию и вычисляется по формуле: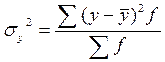 
или 
,
где 
- средняя по всей совокупности; 
- частоты, если по у построен вариационный ряд.
Межгрупповая дисперсия отражает вариацию результативного признака под воздействием фактора, положенного в основу группировки: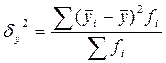 
,
где 
- средняя результативного признака по каждой i- ой группе; 
- частота появления признака в i- ой группе; 
; k -число групп.
Средняя из внутригрупповых дисперсий показывает вариацию результативного признака под воздействием всех факторов, кроме группировочного: 
; 
,
где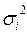 
- внутригрупповая дисперсия или дисперсия i- ой группе; .
Между видами дисперсий существует взаимосвязь, называемая правилом сложения дисперсий: 
= 
+ .
Это правило используется в статистике для определения степени тесноты связи между изучаемыми признаками.
Для количественной оценки тесноты связи между явлениями на основе рассмотренных дисперсий вычисляют ряд показателей, которые будут рассмотрены далее в теме: “Статистические приемы выявления взаимосвязи между социально-экономическими явлениями”.
Показатели формы распределения. Для получения приблизительного представления о форме распределения строят графики распределения (полигон и гистограмму), рассчитываются структурные или ранговые характеристики распределения (квартили, децили), показатели дифференциации, концентрации, асимметрии, эксцесса, а также строятся кривые распределения.
Для сравнительного анализа степени асимметрии нескольких распределений рассчитывается показатель асимметрии (АS):
или 
Наиболее широко (как показатель асимметрии) применяется отношение центрального момента третьего порядка (m3) к среднему квадратическому отклонению в кубе, т.е. 
, 
.
Если 
> 0,то это указывает на наличие правосторонней асимметрии, а при 
, - левосторонней. Чем больше абсолютная величина коэффициента, тем больше степень скошенности распределения.
Оценка существенности AS проводится на основе средней квад-ратической ошибки коэффициента (
): 
.
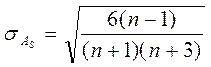Если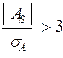 
, асимметрия распределения существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна, и ее наличие может быть вызвано случайными факторами.
Для симметричных распределений рассчитывается показатель эксцесса (островершинности): 
,
где m4 – центральный момент четвертого порядка; m4 = 
.
Эксцесс у высоковершинных распределений положительный, а у низковершинных – отрицательный. Появление значительного отрицательного эксцесса может указывать на качественную неоднородность исследуемой совокупности.
Для оценки существенности коэффициента эксцесса используется его средняя квадратическая ошибка (
): 
.
Если 
, то значение коэффициента эксцесса существенно или статистически значимо.
2. Статистическая проверка гипотез состоит в выявлении согласованности между эмпирическими и гипотетическими (теоретическими) характеристиками. Это могут быть гипотезы о согласованности величины средней, дисперсии, характера распределения, формы и тесноты связи между переменными. Гипотезы принимают, если расхождение между сравниваемыми величинами не выходит за пределы случайных ошибок.
Проверка гипотезы о равенстве средних величин и дисперсий двух совокупностей. Выдвигается нулевая гипотеза | Н0 | о том, что две средни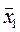е - 
и 
- существенно отклоняются друг от друга при условии примерного равенства дисперсий двух сравниваемых совокупностей.
Рассчитывается: 
или 
; 
По таблицам t -распределения (приложение 1) находим теоретическое значение критерия (tα) по принятому уровню статистической достоверности (α) и числу степеней свободы: m = n – 2,- если tP > tα , то средние существенно отклоняются друг от друга, т.е. нулевая гипотеза не отвергается.
Дополнительно может быть проверена гипотеза о равенстве дисперсий для этих совокупностей. Для этой цели используется критерий Фишера-Снедекора или F -критерий.
Вводим Н0 :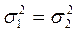 
или альтернативную гипотезу Н1: 
.
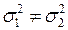F- критерий строится таким образом, чтобы в числителе стояла большая дисперсия, т.е. 
, 
.
По таблицам F -распределения критические значения критерия или его теоретическое значение (
) определяют по заданному уровню значимости (α) и числам степеней свободы сравниваемых дисперсий (m1 = n1 – 1; m2 = n2 – 1) (приложение 2).
Если 
< , то Н0 принимается, а если 
> , то Н0 отвергается, а принимается альтернативная, т.е. Н1 - гипотеза.
Проверка статистических гипотез о законах распределения. Кривая распределения – это кривая линия, которая отражает закономерность изменения частот в чистом, исключающим влияние случайных факторов, виде. В практике статистических исследований часто используется нормальное распределение, распределение Пуассона, бинормальное распределение и др. Каждое теоретическое распределение имеет специфику и свою область применения в различных областях знаний.
Для проверки близости теоретического и эмпирического распределений используются критерии согласия, в частности:
- Критерий согласия К.Пирсона или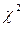 
(хи –квадрат): 
,
где f – эмпирические частоты (или частости);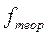 
- теоретические частоты (или частости).
Для нормального закона распределения: 
; 
; 
- определяется по специальной таблице (приложение 3). По таблицам 
-распределения (приложение 4) в зависимости от принятой вероятности (Р) и числа степеней свободы m (m = k – 3, где k - число групп) находим 
,и если 
< 
, то гипотеза о близости эмпирического распределения к нормальному не отвергается.
- На основе 
рассчитывается характеристика критерия В. И. Рома-новского: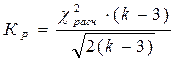 
. Если 
< 3, то можно принять гипотезу о близости эмпирического распределения нормальному.
- Распространенным критерием согласия выступает критерий А.Н.Колмогорова (λ): 
,
где Д – максимальное значение разности между накопленными эмпирическими и теоретическими частотами; n - сумма эмпирических частот.
По таблице вероятностей λ - критерия (приложение 5), определяется вероятность, с которой можно утверждать, случайный или неслучайный характер имеют отклонения фактических частот от теоретических.
Кроме критериев согласия используются также коэффициенты асимметрии и эксцесса. Для нормального закона распределения коэффициенты асимметрии и эксцесса близки к нулю. Распределение можно считать нормальным, если показатели асимметрии и эксцесса не превышают своих двукратных средних квадратических отклонени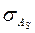й 
и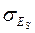 
. Для редко встречающихся явлений характерно распределение Пуассона. Его называют “законом малых чисел”. Теоретические частоты распределения Пуассона рассчитываются по формуле: 
.
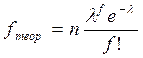где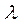 
- среднее число появления редкого события; f - частота данного события; 
- определяется по специальной таблице (приложение 6); f! - произведение 1. 2. 3 … f; 0! =1.
Степень расхождения теоретических и эмпирических частот оценивается с помощью рассмотренных выше критериев согласия.
Тесты
