Групповые средние 
, 
,
где хi и yj – середины соответствующих интервалов; i = 1, 2, …, l; j = 1, 2, …, m; nij – частоты пар (xi, yj); 
; 
.
Общие средние 
, 
,
где 
– объем выборки.
Выборочные дисперсии 
, 
.
Выборочный корреляционный момент или выборочная ковариация 
.
Коэффициенты регрессии Y по X и X по Y 
, 
.
Линейные уравнения регрессии Y по X и X по Y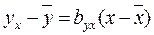 
, 
.
Коэффициент корреляции 
.
20.1. Распределение 100 образцов материала по процентному содержанию синтетической добавки X (%) и предельному напряжению на разрыв Y (Н/cм2) приведены в следующей таблице:
 Y
Х
| 
| ||||||
|
Требуется: 1) найти групповые средние 
и 
и построить эмпирические линии регрессии; 2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессий и построить их графики на одном чертеже с эмпирическими линиями регрессии; б) используя соответствующее уравнение регрессии, найти среднее предельное напряжение на разрыв, когда процент синтетической добавки составляет 50 %, и сравнить его с групповой средней, вычисленной непосредственно по корреляционной таблице.
20.2. Распределение 100 сосен по диаметру ствола Х (см) и высоте Y (м) приведено в следующей таблице:
| Y Х |
| |||||
|
|
Требуется: 1) найти групповые средние и и построить эмпирические линии регрессии; 2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессий и построить их графики на одном чертеже с эмпирическими линиями регрессии; б) используя соответствующее уравнение регрессии, найти средний диаметр сосен высотой 35 м.
20.3. При исследовании корреляционной зависимости между ценой на газ Х и стоимостью акций газовых компаний Y, получены следующие данные: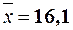 
; 
; 
; 
; m = 40,5. Найти а) уравнения регрессии Y на Х и Х на Y; б) среднюю величину стоимости акции при цене на нефть х = 16,6, используя соответствующее уравнение регрессии.
20.4. Известно, что первоначальная стоимость объекта Х (млн. руб.) и годовая норма отчислений Y (%) связаны уравнениями регрессий: 
и 
. Найти средние значения величин Х и Y, а также коэффициент корреляции между этими величинами.
20.5. При исследовании корреляционной зависимости между объемом валовой продукции Y (млн. руб.) и среднесуточной численностью работающих Х (тыс. чел.) для ряда предприятий получено следующее уравнение регрессии Х на Y: 
. Найти уравнение регрессии Y на Х, если известно, что коэффициент корреляции между этими величинами равен 0,84, а средний объем валовой продукции предприятий составляет 39,8 млн. руб.
20.6. Распределение 100 семей по доходу Х (руб.) на члена семьи и доле расходов на питание Y (%) приведено в следующей таблице:
| Y Х | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | 
|
| 100–500 | ||||||
| 500–900 | ||||||
| 900–1300 | ||||||
| 1300–1700 | ||||||
| 1700–2100 | ||||||
|
|
Требуется: 1) найти групповые средние и построить эмпирические линии регрессии; 2) предполагая, что между переменными Х и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессий и построить их графики на одном чертеже с эмпирическими линиями регрессии; б) используя соответствующее уравнение регрессии, определить среднюю долю расходов на питание при доходе 1300 руб. на члена семьи.
20.7. При исследовании корреляционной зависимости между величинами Х и Y получены следующие данные: 
; 
; 
; 
; m = 50. Написать уравнения регрессии Y на Х и Х на Y и построить графики прямых регрессии.
20.8. При исследовании зависимости между средним баллом аттестата Х и успеваемостью первокурсников Y для ряда вузов получено следующее уравнение регрессии Y на Х: 
. Составить уравнение регрессии Х на Y, если известно, что коэффициент корреляции между этими величинами оказался равным 
, а средняя успеваемость первокурсников составила 3,5 балла.
20.9. При исследовании корреляционной зависимости между возрастом Х (лет) жителей района и числом Y обращений в поликлинику в месяц получены следующие уравнения регрессий: 
и 
. Найти: а) коэффициент корреляции между рассматриваемыми величинами; б) средний возраст и среднее число обращений в поликлинику в месяц жителя района.
ОТВЕТЫ
Элементы комбинаторики
1.1. 10; 1.2. 63; 1.3. 3024; 1.4. 99999; 1.5. 36; 1.6. а) 120, б) 120; 1.7. 1680; 1.8. 5040; 1.9. 2058; 1.10. а) 24310, б) 45; 1.11. 1024000; 1.12. 2520; 1.13. 720; 1.14. 382; 1.15. 125; 1.16. 729; 1.17. 756; 1.18. 300; 1.19. 215760; 1.20. 750.
