Двумерной называют случайную величину (Х, Y), возможные значения которой есть пары чисел (х, у). Составляющие Х и Y, рассматриваемые одновременно, образуют систему двух случайных величин.
Двумерную величину геометрически можно истолковать как случайную точку М(Х, Y) на плоскости хОу, либо как случайный вектор 
.
Функция распределения двумерной случайной величины (Х, Y) определяется соотношением F(x; y) = P(X < x, Y < y) и геометрически определяет вероятность попадания случайной точки (Х, Y) в бесконечный квадрат с вершиной в точке (Х, Y), лежащий левее и ниже ее.
Дискретной называют двумерную величину, составляющие которой дискретны; непрерывной называют двумерную величину, составляющие которой непрерывны.
Законом распределения вероятностей двумерной случайной величины называют соответствие между возможными значениями и их вероятностями.
Закон распределения дискретной двумерной случайной величины может быть задан с помощью таблицы:
| X Y | х1 | х2 | … | хi | … |
| у1 | p11 | p21 | … | pi1 | … |
| у2 | p12 | p22 | … | pi2 | … |
| … | … | … | … | … | … |
| yj | p1j | p2j | … | pij | … |
| … | … | … | … | … | … |
где x1<x2<…<xi<…; y1<y2<…<yj<…;
pij – вероятность события, заключающаяся в одновременном выполнении равенств Х = хi; Y = yj, при этом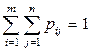 
.
Функция распределения двумерной дискретной случайной величины определяется равенством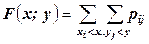 
.
Закон распределения непрерывной двумерной случайной величины может быть задан с помощью функции плотности вероятности f(x,y), удовлетворяющей условиям:
1) f(x; y) ³ 0; 2) 
.
Если все возможные значения (Х, У) принадлежат конечной области D, то 
.
Вероятность попадания случайной точки (Х, У) в область D определяется равенством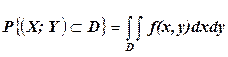 
.
Связь плотности вероятности f(x, y) и функции распределения F(x,y) двумерной непрерывной случайной величины задается соотношениями 
; 
.
Законы распределения составляющих непрерывной двумерной случайной величины вычисляются по формулам 
; 
.
Для нахождения законов распределения составляющих двумерной дискретной случайной величины надо суммировать вероятности в таблице по строкам или по столбцам.
Условным распределением составляющей Х при Y = уj (j – сохраняет одно и то же значение при всех возможных значения Х) называют совокупность условных вероятностей 
, 
, …, 
.
Аналогично определяется условное распределение Y. Условные вероятности составляющих X и Y вычисляются соответственно по формулам
; 
.
Для непрерывных случайных величин формулы вычисления условных плотностей распределения выглядят так:
; 
.
Числовые характеристики составляющих вычисляются по формулам:
; 
– для дискретных случайных величин;
; 
– для непрерывных случайных величин;
; 
;
; 
.
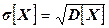Точка 
называется центром рассеяния двумерной случайной величины (X, Y).
Для оценки тесноты взаимосвязи составляющих вычисляют корреляционный момент или ковариацию 
.
Корреляционный момент удобно вычислять по формуле 
, где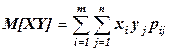 
в дискретном и 
в непрерывном случае.
Степень связи между составляющими в чистом виде характеризует так называемый нормированный корреляционный момент или коэффициент корреляции 
, обладающий следующими свойствами: 1) 
2) 
тогда и только тогда, когда случайные величины связаны линейной зависимостью.
Случайные величины Х, У называются некоррелированными, если КXY = 0, а следовательно, и 
.
Случайные величины Х, Y называются независимыми, если вероятность одной из них принять значение, лежащее в любом промежутке области ее значений, не зависит от того, какое значение приняла другая величина.
Для двумерной дискретной случайной величины, представленной в виде таблицы распределения, условие независимости составляющих Х и Y состоит в том, что для любых i и j 
, где 
, 
. Внешне это выражается в том, что строки и столбцы таблицы пропорциональны.
Для двумерной непрерывной случайной величины условие независимости состоит в том, что 
.
Независимые случайные величины всегда некоррелированны. Обратное, вообще говоря, неверно (т.е. некоррелированные величины могут быть зависимыми).
Условным законом распределения случайной величины Yx называется закон распределения случайной величины Y при условии, что Х = х.
Функциональная зависимость М[Yx] = j(x) называется регрессией случайной величины Y на случайную величину Х.
Среднее значение квадрата отклонения 
достигает минимально возможного, когда j(х) – регрессия Y на Х (минимизирующее свойство регрессии).
Функция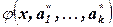 
из класса функций 
определяемых набором параметров а1, …, аk называется среднеквадратичной регрессией Y на Х в этом классе функций, если среднее значение квадрата отклонения 
достигает на наборе параметров 
минимального значения для всех функций этого класса.
Простейшей функцией является линейная: 
. Уравнение прямой среднеквадратичной регрессии Y на Х выглядит так: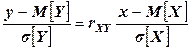 
.
Аналогично уравнение прямой среднеквадратичной регрессии Х на Y: 
.
16.1. Восстановить законы распределения составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Найти условное распределение случайной величины Х при условии, что Y = y1. Найти условное распределение случайной величины Y при условии, что Х = х2.
| Х Y | |||
| 0,2 | 0,18 | 0,22 | 0,16 |
| 0,8 | 0,08 | 0,16 | 0,2 |
16.2. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины.
| Х Y | 0,8 | 1,5 | |
| 0,2 | 0,2 | 0,1 | |
| 0,2 | 0,1 | 0,2 |
16.3. По некоторой цели производится два выстрела. Вероятность попадания при одном выстреле равна 0,7. Составить таблицу распределения двумерной случайной величины (Х; Y), где Х – число попаданий, Y – число промахов. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Определить, зависимы или нет составляющие Х и Y.
16.4. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной непрерывной случайной величины (Х; Y), имеющей плотность 
, где D – треугольник ограничен-ный линиями: х = 0; у = 0; х + у = 1. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения 
.
16.5. Двумерная непрерывная случайная величина (Х; Y) подчинена закону распределения с плотностью 
, где D – квадрат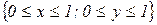 
. Найти коэффициент а. Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
16.6. Двумерная непрерывная случайная величина (Х; Y) распределена равномерно в круге радиуса R = 5 с центром в начале координат. Доказать, что составляющие Х и Y являются зависимыми и некоррелированными величинами.
16.7. Найти плотность вероятности f(x; y) двумерной случайной величины (Х; Y), имеющей функцию распределения 
.
16.8. Найти уравнения прямых линий средних квадратических регрессий Y на Х и Х на Y двумерной случайной величины (Х; Y), заданной таблицей распределения:
| Х Y | 0,2 | 0,5 | |||||
| 0,3 | 0,1 | ||||||
| 1,5 | 0,2 | 0,1 | |||||
| 0,1 | 0,2 | ||||||
16.9. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной дискретной случайной величины (Х; Y), заданной таблицей распределения. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины.
| Х Y | 0,5 | ||
| 0,5 | 0,2 | 0,1 | 0,2 |
| 0,1 | 0,3 | 0,1 |
16.10. Найти числовые характеристики M[X], D[X], s[X], M[Y], D[Y], s[Y] составляющих Х и Y двумерной непрерывной случайной величины (Х; Y), имеющей плотность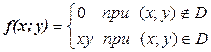 
, где D – прямоугольник 
. Вычислить корреляционный момент и коэффициент корреляции данной случайной величины. Найти функцию распределения .
16.11. Двумерная непрерывная случайная величина (Х; Y) подчинена закону распределения с плотностью 
, где D – квадрат 
. Определить, зависимы или нет составляющие Х и Y. Найти коэффициент корреляции и условные законы распределения Х, Y.
16.12. Найти плотность вероятности f(x; y) двумерной случайной величины (Х; Y), имеющей функцию распределения 
.
16.13. Найти уравнения прямых линий средних квадратических регрессий Y на Х и Х на Y двумерной случайной величины (Х; Y), заданной таблицей распределения:
| Х Y | 1,5 | ||
| 0,3 | 0,1 | 0,1 | |
| 0,1 | 0,2 | ||
| 0,1 | 0,1 |
Функции случайных величин
Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайной величины Х и записывают Y = j(х).
Если Х – дискретная случайная величина, то возможные значения Y находят из равенства уi = j(xi), где xi – возможные значения Х; вероятности возможных значений Y находят из равенства P{Y=yi} = P{X=xi}. Если среди возможных значений Y встретятся одинаковые, то следует сложить вероятности тех возможных значений Х, при которых Y принимает одинаковые значения.
Если Х – непрерывная случайная величина с плотностью вероятности fx(x), а у = j(х) – дифференцируемая строго монотонная функция, обратная функция которой х = y(у) однозначна, то плотность вероятности fy(y) случайной величины Y определяетcя по формуле 
.
Если функция Y= j(х) не монотонная в интервале возможных значений Х, то следует разбить этот интервал на такие интервалы, в которых функция j(х) монотонна, найти плотность распределения Y для каждого интервала монотонности, а затем представить fy(y) в виде их суммы 
.
Числовые характеристики функции случайной величины можно найти, не определяя закона распределения у = j(х) по формулам
;
для дискретных случайных величин и
;
для непрерывных случайных величин.
Аналогично находятся начальные и центральные моменты любого порядка, а также числовые характеристики функции нескольких случайных аргументов (подробнее см. [8]).
Если функция j(Х1, Х2, …, Хn) – линейная, т.е. 
, то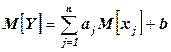 
; 
,
где Кij – корреляционный момент случайных величин Хi и Xj (в этом случае не требуется знание закона распределения случайных аргументов).
Числовые характеристики непрерывно дифференцируемых функций могут быть вычислены приближенно методом линеаризации (т.е. удерживая в разложении функции в ряд Тейлора только линейные члены):
а) для функции одного случайного аргумента Y = j(х)
M[Y]» j(M[x]); D[Y]» [j’(M[x])]2D[x];
б) для функции нескольких случайных аргументов Y = j(Х1, Х2,…, Хn)
М[Y]» j(M[Х1], M[Х2], …,M[Хn]),
,
где Кij – корреляционный момент для случайных величин Хi и Xj, а через 
обозначены производные, вычисленные для значений аргументов, равных их математическим ожиданиям.
Если случайные величины взаимно не коррелированны, то 
.
17.1. Дискретная случайная величина имеет ряд распределения:
| x | 
| 
| 
| 
| 
| |
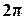
| р | 0,1 | 0,2 | 0,1 | 0,2 | 0,3 | 0,1 |
Найти закон распределения функции z = sinx, вычислить M[Z] и D[Z].
17.2. Непрерывная случайная величина Х имеет плотность вероятности f(x). Выразить функцию распределения и плотность вероятности случайной величины Z = x 2 через функцию и плотность распределения Х.
17.3. Независимые случайные величины Х и Y распределены показательно с параметрами a и b соответственно a ¹ b. Найти плотность вероятности случайной величины Z = X + Y.
17.4. Система состоит из двух независимых элементов, соединенных последовательно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
Указание. T = min {T1, T2}, где T i – время безотказной работы i -го элемента.
17.5. Система состоит из двух независимых элементов, соединенных параллельно в смысле надежности. Время безотказной работы каждого из элементов имеет показательное распределение с параметрами a1 и a2 соответственно. Найти функцию распределения времени безотказной работы системы.
Указание. T = max {T1, T2}, где T i – время безотказной работы i -го элемента.
17.6. Непрерывная случайная величина имеет плотность 
Найти математическое ожидание и дисперсию случайной величины Y = sin X
17.7. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | y | ||||||
| р | 0,2 | 0,5 | 0,3 | р | 0,4 | 0,6 |
Найти закон распределения случайной величины Z = X – 2Y и проверить свойства математических ожиданий и дисперсией M[Z] = M[X ]– 2M[Y], D[Z] = D[X]+4D[Y].
17.8. Результат измерения ребра куба есть случайная величина Х, дисперсия которой (характеристика точности измерительного прибора) равна 0,0001 мм2. Определить приближенно дисперсию объема куба Y, вычисляемого по результатам измерений, если измеряемые прибором длины заключены в пределах от 1 мм до 2 мм.
17.9. Начальная фаза j малых свободных колебаний груза на пружине связана с начальным смещение Х, начальной скоростью v и свободной круговой частотой колебаний w формулой 
. Начальные условия задаются независимо с разбросом относительно номинальных значений mx = 2 см и mv = 2 см/с, который характеризуется средними квадратическими отклонениями sх = 0,4 см, sv = 0,3 см/с. Вычислить приближенно среднее квадратическое отклонение начальной фазы при w = 10.
17.10. Размеры двух шкивов (А и В) характеризуются математическими ожиданиями радиусов (номинальные размеры)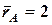 
, 
и дисперсиями исполнения D[ rA ] = 0,04, D[ rB ] = 0,01. Найти приближенно математическое ожидание и среднее квадратическое отклонение передаточного числа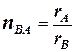 
от шкива В к шкиву А.
 |
17.11. Линейная размерная цепь включает в себя три составляющих размера Х, Y, Z и замыкающий размер Т. Соответствующие номинальные размеры равны: 
= 100 мм, 
= 50 мм, 
= 250 мм. Кроме того, известно, что sх = 1 мм, sу = 1 мм, sz = 2 мм. Размер Z получается независимой от Х и Y обработкой, а размеры Х и Y получаются согласно технологии связанными, причем rxy = 0,9. Найти М[T], s[T].
 |
 |
 |
17.12. Кинематика кривошипно-кулисного механизма определяется размерами h и r, при исполнении которых допускаются погрешности, характеризующиеся средними квадратическими отклонениями sh и sr . Найти номинальный максимальный угол отклонения кулисы jmax от вертикального положения и среднее квадратическое отклонение реального угла, если номинальные размеры r и h равны соответственно 141,4 мм и 200 мм, sh = 1 мм, sr = 2 мм.
Указание. 
.
17.13. Пусть Х – непрерывная случайная величина с плотностью f(x). Выразить плотность вероятности функции z = a X + b (a > 0) через f(x).
17.14. Две независимые случайные величины Х и Y имеют следующие законы распределения:
| х | –4 | y | ||||||
| р | 0,2 | 0,6 | 0,2 | р | 0,5 | 0,2 | 0,3 |
Найти закон распределения случайной величины Z = 2X – Y и проверить свойства математических ожиданий и дисперсией M[Z] = 2M[X ]– M[Y], D[Z] = 4D[X]+D[Y].
17.15. Колебательная система состоит из груза с массой m = 1 кг и пружины с жесткостью k = 4 Н/м. Она выводится из состояния равновесия случайным смещением Х0, распределенным равномерно на отрезке [ –0,1 м; 0,1 м] и случайным Р0 = m v0, математическое ожидание которого 
= 2 кг м/с, среднее квадратическое отклонение 
= 1 кг м/с. Найти приближенно математическое ожидание и дисперсию амплитуд малых свободных колебаний.
Указание. Амплитуда свободных колебаний связана с начальными условиями соотношением 
.
17.16. При измерении стороны квадрата линейкой, цена деления которой равно 2D, допускается погрешность округления. Пусть длина стороны квадрата равна а. Найти плотность вероятности случайной величины S – результата вычисления площади квадрата. Вычислить математическое ожидание и дисперсию S и сравнить полученные точные значения с приближенными, определенными по методу линеаризации.
Указание. Результат измерения Х есть случайная величина, равномерно распределенная на отрезке [ а– D; а +D].
17.17. По сторонам прямого угла xОy концами скользит линейка АВ длины l, занимая случайное положение, причем все значения абсциссы X её конца А на оси Ох в пределах от 0 до l одинаково вероятны. Найти математическое ожидание расстояния R от начала координат до линейки.
Закон больших чисел
Под законом больших чисел понимается ряд теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Рассмотрим вспомогательные теоремы: лемму и неравенство Чебышева, с помощью которых доказывается закон больших чисел в форме Чебышева.
Лемма Чебышева. Если случайная величина Х принимает только неотрицательные значения и имеет математическое ожидание, то для любого положительного числа А верно неравенство
или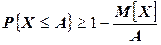 
.
Неравенство Чебышева. Для любой случайной величины, имеющей математическое ожидание и дисперсию, справедливо неравенство
или 
.
Для некоторых случайных величин неравенство Чебышева записывается так:
a) для случайной величины X, имеющей биномиальный закон распределения с математическим ожиданием 
и дисперсией 
:
;
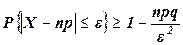б) для частости 
события в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью 
, и имеющей дисперсию 
:
.
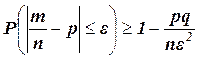Теорема Чебышева. Если дисперсии n независимых случайных величин X1 , X2 , …, Xn ограничены одной и той же постоянной, то при неограниченном увеличении числа n средняя арифметическая случайных величин сходится по вероятности к средней арифметической их математических ожиданий a1, a2, …, an, т.е.
.
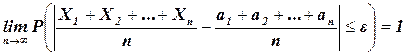Следствие. Если независимые случайные величины X1, X2, …, Xn имеют одинаковые математические ожидания, равные а, а их дисперсии ограничены одной и той же постоянной С, то
.
18.1. Среднее число вызовов, поступающих в течение часа на станцию скорой помощи, равно 30. Оценить вероятность того, что в течение часа число вызовов: а) превысит 40; б) не превысит 50.
18.2. Фонд заработной платы учреждения составляет 200 тыс. руб., а вероятность того, что зарплата случайно взятого сотрудника не превысит 1000 рублей, равна 0,6. Оценить численность персонала учреждения.
18.3. Средний расход воды в садоводческом товариществе составляет 200 м3 в день, а среднее квадратическое отклонение этой случайной величины равно 40 м3. Оценить вероятность того, что в какой-то день расход воды в товариществе не превысит 400 м3, используя а) лемму Чебышева; б) неравенство Чебышева.
18.4. Вероятность своевременной доставки почтового отправления адресату равна 0,98. Оценить с помощью неравенства Чебышева вероятность того, что число несвоевременно доставленных среди 1000 почтовых отравлений находится в границах от 10 до 30 (включительно). Уточнить вероятность того же события с помощью интегральной теоремы Муавра-Лапласа.
18.5. Дисперсия отдельного измерения некоторой величины не превосходит 2. Сколько надо провести измерений величины, чтобы с вероятностью, не меньшей 0,95, гарантировать отклонение средней арифметической этих измерений от истинного значения величины не более чем на 0,1 (по абсолютной величине)?
18.6. На основании длительных наблюдений за спортивными достижениями легкоатлета составлена следующая таблица его результатов в беге на 100 м:
| Время, показанное спортсменом, в сек. | 10,5 | 11,5 | |||
| Вероятность | 0,1 | 0,3 | 0,5 | 0,05 | 0,05 |
С помощью леммы Чебышева оценить вероятность того, что легкоатлет на стометровке покажет время хуже 12 секунд.
18.7. Даны 50 независимых неотрицательных случайных величин Х1, Х2, …, Х50 с математическими ожиданиями М[Х i ] = 0,5 и дисперсиями D[X i ] = 0,5 (i = 1, 2, …, 50). С помощью неравенства Чебышева оценить вероятность того, что средняя арифметическая этих случайных величин не превзойдет величины, равной 1.
18.8. По данным переписи населения в среднем 90 % семей имеют холодильники. С помощью неравенства Чебышева оценить вероятность того, что из 1000 семей доля семей, имеющих холодильник, будет отличаться от вероятности этого события не более чем на 0,04 (по абсолютной величине).
18.9. Опрос показал, что адресная реклама в среднем в каждом пятидесятом случае приводит к тому, что потенциальный покупатель приобретает рекламируемый товар. С помощью неравенства Чебышева найти границы, в которых будет находиться число сделанных по рекламе заказов, если всего разослано 10000 рекламных листков.
18.10. Продолжительность горения электролампочки является случайной величиной, дисперсия которой не превышает 8100. Пользуясь теоремой Чебышева, оценить наибольшее отклонение средней арифметической продолжительности горения 4000 электролампочек от средней арифметической их математических ожиданий, если результат необходимо гарантировать с вероятностью, не меньшей 0,9.
18.11. Практика показывает, что 7 % накладных, проходящих проверку в бухгалтерии, оказываются неправильно оформленными. Используя неравенство Чебышева, оценить вероятность того, из 500 накладных доля правильно оформленных окажется от 0,91 до 0,95.
18.12. Для определения среднего веса пакета со стиральным порошком в партии из 100 коробок было взято на выборку по одному пакету из каждой коробки. Оценить вероятность того, что средний вес отобранных 100 пакетов отличается от среднего веса пакета во всей партии не более чем на 10 г (по абсолютной величине), если известно, что среднее квадратическое отклонение веса пакета в каждой коробке меньше 18 г.
3. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА
Основы выборочного метода
Обозначения:
xi – значения признака (случайной величины Х);
N и n – объемы генеральной и выборочной совокупностей;
Ni и ni – число элементов генеральной и выборочной совокупностей со значением признака хi;
M и m - число элементов генеральной и выборочной совокупностей, обладающих данным признаком.
Таблица 1. Расчет характеристик генеральной и выборочной совокупностей.
| Наименование характеристики | Генеральная Совокупность | Выборка |
| Средняя | 
| 
|
| Дисперсия | 
| 
|
| Доля | 
| 
|
Важнейшей задачей выборочного метода является оценка параметров (характеристик) генеральной совокупности по данным выборки.
Таблица 2. Оценка параметров генеральной совокупности
по собственно-случайной выборке.
| Параметр | Выборка | Несмещенная и состоятельная оценка | Дисперсия оценки |
| Генеральная доля | Повторная |
| 
|
| Бесповторная |
| 
| |
| Генеральная средняя | Повторная | 
| 
|
| Бесповторная |
| 
| |
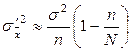
| Генеральная дисперсия | Повторная и бесповторная |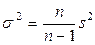 
|
Среднее квадратическое отклонение выборочной средней 
и выборочной доли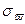 
собственно-случайной выборки называется средней квадратической (стандартной) ошибкой выборки. (Для бесповторной выборки обозначения – соответственно 
и 
).
Формулы доверительной вероятности для средней 
и доли 
.
При заданной доверительной вероятности g предельная ошибка выборки равна t-кратной величине средней квадратической ошибки, где 2F0(t) = g, т.е. 
, 
.
Интервальные оценки (доверительные интервалы) для генеральной средней и генеральной доли могут быть найдены по формулам: 
, 
.
Таблица 3. Формулы средних квадратических ошибок выборки
| Оцениваемый параметр | Повторная выборка | Бесповторная выборка |
| Генеральная средняя | 
| 
|
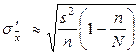
| Генеральная доля | 
| 
|
Таблица 4. Определение объема выборки по доверительной вероятности g
и предельной ошибке выборки D
| Оцениваемый параметр | Повторная выборка | Бесповторная выборка |
| Генеральная средняя | 
| 
|
| Генеральная доля | 
| 
|
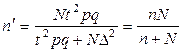
19.1. Отдел технического контроля электролампового завода хочет узнать срок службы (время горения) отдельного вида лампочек. С этой целью случайная выборка 80 лампочек была испытана на продолжительность горения. Выборочная средняя равняется 2915 час, а выборочное среднее квадратическое отклонение 396 час. Найти вероятность того, что средний срок службы лампочек данного вида отличается от выборочной средней не более, чем на 90 час (по абсолютной величине).
19.2. Случайная выборка 800 школьников показала, что 480 из них хотела бы заниматься в школе в первую смену. Определить границы, в которых с вероятностью 0,9 заключена доля всех школьников, которые хотели бы учиться в первую смену.
19.3. Отдел сбыта кондитерской фабрики при опросе 200 жителей города А, отобранных по схеме собственно-случайной бесповторной выборки, обнаружил, что для 50 из них желательно изменение ассортимента продукции. Отдел наметил провести такое же обследование в городе Б. Найти: а) 95 %-й доверительный интервал для доли потребителей в городе А, которые будут покупать новые виды продукции; б) объем выборки в городе Б, чтобы достичь оценки доли потребителей новой продукции в пределах ± 4 % с доверительной вероятностью 0,95.
19.4. По схеме собственно-случайной бесповторной выборки было отобрано 100 студентов из 500 обучающихся и получены следующие данные о времени решения задачи по теории вероятностей:
| Время решения задачи, мин. | |||||
| Количество студентов |
Найти: а) вероятность того, что среднее время решения задачи в выборке отличается от среднего времени решения задачи во всей генеральной совокупности не более чем на 1 минуту (по абсолютной величине); б) число студентов, которое нужно отобрать в выборку, чтобы то же отклонение гарантировать с вероятностью 0,9876; в) границы, в которых с вероятностью 0,9596 заключена доля студентов, решавших задачу не более 9 минут.
19.5. Для определения рейтинга мэра города было опрошено 200 человек. Выборочный рейтинг оказался равным 0,4. Определить необходимое количество респондентов, гарантирующее с вероятностью 0,9802 ошибку социологического обследования, не превосходящую 2 %.
19.6. Проводится сравнительный анализ старого и нового метода сборки некоторого изделия. Среднее время сборки по старому методу составляет 90 мин. Для оценки нового метода сборки по схеме бесповторной собственно-случайной выборки были отобраны 100 рабочих из 500. Получено следующее распределение рабочих по продолжительности сборки:
| Продолжительность сборки, мин. | |||||
| Число рабочих |
Найти: а) доверительный интервал с вероятностью 0,95 для среднего времени сборки по новому методу; б) наименьший размер выборки, необходимый для получения среднего значения генеральной совокупности в пределах двух минут с доверительной вероятностью 0,9901.
19.7. Маркетинговое исследование показало, что реализуемый фирмой товар требуется 16 из 200 опрашиваемых. Фирма разворачивает свою деятельность в районе с населением 20000 человек. Найти границы, в которых с вероятностью 0,95 будет заключено количество покупателей.
19.8. Торговая фирма получила от поставщика пробную партию из 100 стиральных машин. Среди них оказалось 5 с дефектами. Найти вероятность того, что доля стиральных машин с дефектами во всей партии из 5000 штук отличается от таковой в выборке не более чем на 0,02.
19.9. Из 620 студентов-первокурсников БГТУ было отобрано по схеме собственно-случайной бесповторной выборки 100 студентов, из которых оказалось 60 проживающих в г. Брянске. Найти границы, в которых с вероятностью 0,9545 заключен процент студентов – жителей г. Брянска среди всех студентов первого курса.
19.10. По схеме собственно-случайной бесповторной выборки из общего большого числа стальных проволок, идущих на изготовление канатов, были отобраны 150 и проведены испытания на растягивающее усилие. Оказалось, что проволока выдерживает в среднем усилие в 67,2 кН/см2 , а выборочное среднее квадратическое отклонение равно 2,2 кН/см2. Найти: а) границы, в которых с вероятностью 0,9975 заключено среднее разрывное усилие проволок всей партии; б) вероятность того, что среднее разрывное усилие всех проволок в партии не отличается от среднего разрывного усилия в выборке не более чем на 0,3 кН/см2; в) объем выборки, для которой доверительные границы с предельной ошибкой D = 0,5 имели бы место с доверительной вероятностью 0,9910.
